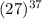Для начала выясним, что же будет графиком этой функции? В данном случае парабола, при чем, т.к. перед x^2 стоит знак "-", то ветви направлены вниз. Значит, эта функция будет принимать значения от минус бесконечности, до ординаты вершины параболы. Задание сводится к тому, чтобы найти координаты вершины. Приступим.
Абсциссу вершины параболы находив по формуле:
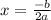, где b-коэффициент перед x, а-коэффициент перед x^2.
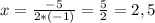
Теперь подставим значение икса в нашу функцию и найдем ординату вершины параболы
y=-(2,5)^2 +5*2,5-9=-6,25 +12,5-9=-6,25+3,5=-2,75=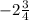
Значит координаты вершины параболы (2,5; -2,75)
Следовательно, функция принимает значения ![(- \infty;-2\frac{3}{4}]](/tpl/images/0091/8443/7c376.png)
Вопрос не до конца написан. Я так полагаю, что нужно найти количество нужных пачек.
Итак, меньшую сторону возьмём за Х, тогда большая сторона будет x+7
Площадь равна произведению двух сторон, получаем уравнение x*(x+7) = 170 или X²+7x-170=0. х=10 и х=-17, Сторона не может быть отрицательной, соответственно длина меньшей стороны площадки будет 10м. Длина большей стороны 10+7=17м. Находим периметр: 10+10+17+17 = 54м. Находим количество пачек: 54м÷22м=2 с чем-то, но округлить нужно в большую сторону, соответственно 3. Получается, что для бордюра нужно будет 3 пачки материала.
Объяснение:
4) 40²⁰×40³=40^23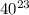
5) (0,3)⁷×(0,3)²⁹=(0,3)^36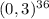
6) (8,4)³×(8,4)¹⁵=(8,4)^18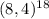
7) ( 2/7)³¹× ( 2/7)⁶=(2/7)^37