Докажем сначала, что корень единственный. Для этого исследуем функцию
корни производной
В точке функция имеет локальный максимум, в точке - локальный минимум, после него функция монотонно растет.
так как корень из двух меньше, чем 1,5. Итак, слева от функция возрастает, справа убывает, начиная с снова возрастает. Поскольку функция в точке отрицательна, существует только один корень функции (и расположен он правее ; для нас, правда, важна только его единственность).
Возвращаемся к уравнению Для его решения применим метод Кардано. Замена после элементарных упрощений получаем уравнение
Вроде бы надо исследовать оба значения p, однако оба они дадут одно и то же значение t (кстати, ранее мы даже доказали, что двух решений быть не может). Итак, пусть p=2;
Чтобы парабола не имела решений надо чтобы ее значение было всегда больше нуля при любых x при некоторых тк парабола всегда положительна то если рассуждать графически то она не должна пересекать оси абсцис тк вышло бы что она может принимать и пол и отриц знач а тогда чтобы этого не произошло ее ветви должны быть расположены вверх то есть a>0 ,но тк a=1 то это условие выполняется.но тут есть еще 1 условие чтобы yв>0 то есть ее минимальное значение было выше оси обсцис.оно не может лежать на ней тк в задании неравенство строгое ,а решений быть не должно. Таким образом должно вы подняться неравенство yв=-d/4a чтоD=(2a+3)^2-4*(6a+1)=4a^2-12a+5 тогда yв=-4a^2+12a-5/4>0 умножим обе части на -4 получим не забывая менять знак неравенства 4a^2-12a+5<0 ищем корни нашего трехчлена D/4=36-20=16=4^2 a1=(6+4)/4=2,5 a2=(6-4)/4=1/2 раставляем знаки на координатной прямой в итоге нужный интервал где стоит минус a{0,5;2,5} то есть ответ :a{0,5;2,5} надеюсь понятно объяснил?
Докажем сначала, что корень единственный. Для этого исследуем функцию
В точке
функция имеет локальный максимум, в точке 
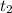- локальный минимум, после него функция монотонно растет.
Возвращаемся к уравнению
Для его решения применим метод Кардано. Замена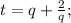 
после элементарных упрощений получаем уравнение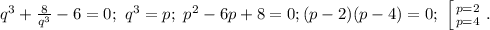 
Вроде бы надо исследовать оба значения p, однако оба они дадут одно и то же значение t (кстати, ранее мы даже доказали, что двух решений быть не может). Итак, пусть p=2;![q=\sqrt[3]{2};\ t=\sqrt[3]{2}+\frac{2}{\sqrt[3]{2}}=\sqrt[3]{2}+\sqrt[3]{4}; x=2+\sqrt[3]{2}+\sqrt[3]{4}](/tpl/images/0199/1839/61451.png)
ответ:![2+\sqrt[3]{2}+\sqrt[3]{4}](/tpl/images/0199/1839/f6929.png)