Решение на фотографии.
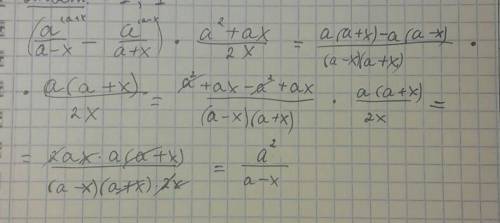, я могу и вам." />
Школьные Знания.com
Какой у тебя вопрос?
annashayuk
10 - 11 классыМатематика 5+3 б
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Отметить нарушение Kvsrvl 22.09.2016
ответы и объяснения
ЛУЧШИЙ ОТВЕТ!
vmaluga2011
Vmaluga2011 Главный мозг
48 мин=48:60=4/5 (часа) (1 час=60 мин)
Расстояние между А и В - 1
х часов ехал велосипедист
V=S:t
1/х - скорость велосипедиста
х-3 часов ехал мотоциклист
1:(х-3) - скорость мотоциклиста
S=Vt
1/х*4/5=4/5х - проехал велосипедист до встречи
1:(х-3)*4/5=4:(5х-15) - проехал мотоциклист до встречи
4/5х+4:(5х-15)=1
4(5х-15)+4*5х=5х(5х-15) Разделим обе части ур-ия на 5
4(х-3)+4х=х(5х-15)
4х-12+4х=5х2-15х
5х2-23х+12=0
D=23*23-4*5*12=529-240=289 Корень из D=17
х"=(23-17):10=6/10=3/5 (не подходит по условию)
х=(23+17):10=40:10=4 (часа)
ответ: велосипедист потратил на дорогу из В в А 4 часа
2,5,6,8
Объяснение:
Пусть Петя загадал число x. Тогда у Васи получилось число x + 1, а у Коли — x - 1. Тогда полученное произведение имеет вид x(x + 1)(x - 1)
1 — неверно. Например, при x = 2 произведение чётное, один из множителей (x) делится на 2.
2 — верно. Докажем, что произведение всегда делится на 2: если x — чётное число, то произведение делится на 2, если x — нечётное число, то x + 1 — чётное число, и произведение также делится на 2. Докажем, что произведение всегда делится на 3: если x делится на 3, то всё произведение делится на 3, если x имеет остаток 1 при делении на 3, то x - 1 делится на 3, если x имеет остаток 2 при делении на 3, то x + 1 делится на 3 — во всех возможных случаях находится множитель, кратный трём. Значит, произведение всегда делится на 2·3 = 6.
3 — неверно. Например, при x = 2 произведение равно 6, его сумма цифр не делится на 9.
4 — неверно. Оно всегда чётное, то есть делится на 2. Доказательство приведено в п. 2.
5 — верно. Произведение всегда делится на 3 (доказательство приведено в п. 2), значит, и его сумма цифр делится на 3.
6 — верно. Доказательство приведено в п. 2.
7 — неверно. Например, при x = 1 произведение равно 1·2·0 = 0 < 1.
8 — верно. Произведение имеет вид 2021·2022·2020. 2020 делится на 4, 2022 делится на 2, значит, произведение делится на 8.
Объяснение:
1. (a/(a-x)-a/(a+x)=(a*(a+x)-a*(a-x)/((a-x)*(a+x))=
=(a²+ax-a²+ax)/((a-x)*(a+x))=2ax/((a-x)*(a+x)).
2.2ax/((a-x)*(a+x))*(a²+ax)/(2x)=2ax*(a*(a+x))/(2x*(a-x)*(a+x))=a²/(a-x).