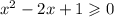
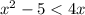
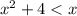
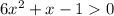
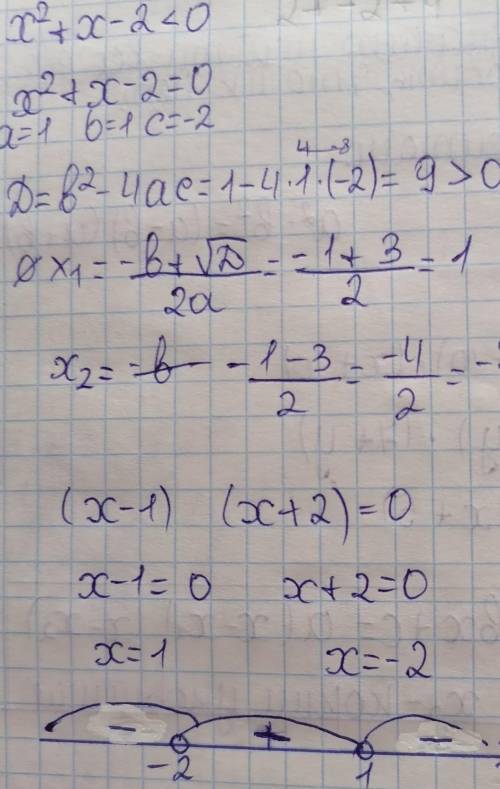
Объяснение:
1. 5(2×0,6+1)-3=5(1,2+1)-3=5×2,2-3=11-3=8
2.а) 5х^3×(-2х^2)=-10х^5
б) 2а-(6в-а)+(6в-2а) = 2а-6в+а+6в-2а=а
в)(3x - 1)(3x + 1) + - (3x + 1)^2 = 9x^2 + 1 - 9x^2 + 6x + 1 = 6x + 2
г)(2х^3у)^3=8х^9у^3
3. а)2ху-6у^2=2у(х-3у)
б) а^5-4а^3=а^3(а^2-4)
в) а^3-2а^2+18-9а=а^2(а-2)+9(2-а)
4. а) 4(2-4х)=3-6х
8-16х=3-6х
-16х+6х=3-8
-10х=-5
х=-5÷(-10)=0,5
б) (х-1)(х+7)=0
х^2+7х-х-7=0
х^2 +6х-7=0
за теоремой Виета
х1+х2=-6
х1×х2= -7. х1=-7. х2=1
в) 2у^2-18=0
2у^2=18
у^2=9
у=3;у=-3
5. 1 день -х
2 день - х-10
3 день - х-10-5
х+х-10+х-10-5= 50
3х -25=50
3х=75
х= 25
1день 25км
2 день 15км
3день 10км
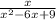 -
-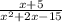
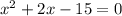
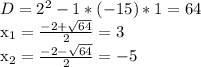
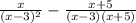
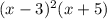 Вот он
Вот он 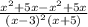
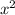 -сокращаем
-сокращаем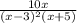
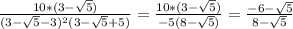
1) x²-2x+1 ≥ 0
x²-2x+1 = 0
a = 1 , b = -2, c = 1
D = b²-4ac ; D = (-2)² - 4*1*1 = 4-4 = 0 ⇒ у уравнения один корень
(x-1)² = 0
Точка будет закрашена, т.к. уравнение нестрогое
- +
-------------·--------------->
1
ответ: х∈[1;+∞)
2) x²-5 < 4х
x²-4х -5 < 0
x²-4х -5 = 0
a = 1 , b = -4, c = -5
D = b²-4ac ; D = (-4)² - 4*1*(-5) = 16+20 = 36 = 6² ⇒ у уравнения два корня
(x-5)(х+1) = 0
Точки не будут закрашены, т.к. уравнение строгое
+ - +
--------₀----------₀---------->
-1 5
ответ: х∈(-1;5)
3) x²+4 < х
x²-х+4 < 0
x²-х+4 = 0
a = 1 , b = -1, c = 4
D = b²-4ac ; D = (-1)² - 4*1*4 = 1-16 = -15 ⇒ у уравнения нет корней
ответ: х∉R
4) 6x²+x-1 > 0
6x²+x-1 = 0
a = 6 , b = 1, c = -1
D = b²-4ac ; D = 1² - 4*6*(-1) = 1+24 = 25 = 5² ⇒ у уравнения два корня
Точки не будут закрашены, т.к. уравнение строгое
+ - +
--------₀----------₀---------->
ответ: х∈(-∞;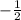 )∪(
)∪(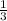 ;+∞)
;+∞)