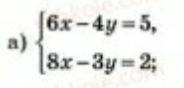
Объяснение:
{6x-4y=5 // * 4
{8x-3y=2 // * (-3)
{24x-16y=20
(+){-24x+9y=-6
.
-7y=14 // : (-7)
Y=-2 подставляем в (1) уравнение: 6x-4y = 5
6x-4(-2)=5
6x+8=5
6x=5-8
6x=-3 // : 6
X= -1/2
OTBET: решение системы уравнений представляет собой пару чисел {x = -1 / 2
{y = -2
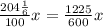
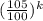 .
.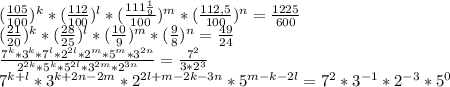
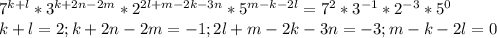
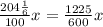
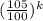 .
.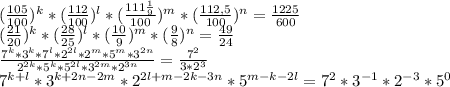
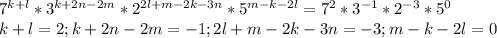
66 - 41 =5 86 - 34 =2
Я так понял
Объяснение: