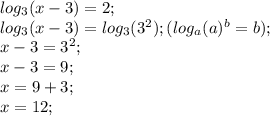
Все очень просто, двойку представляем как log3(3^2); Т.к. с двух сторон логарфимы с одинаковым основанием мы имеем право "отбросить" их. Далее - обычная арифметика.
Можно сделать проверку, на правильность нахождения корня. (С более сложными уравнениями она понадобится, ибо бывают "ложные" корни, при которых не выполняется равенство уравнения).
Подставляем значение 12 вместо икса:
log3(12-3)=2;
log3(9)=2;
log3(3)^2=2;
Согласно вышесказанной формуле, получаем:
2=2.
Корень найден нами верно. (Хотя другого варианта и не могло быть в данном уравнении).
ответ: x=12.
Объяснение:
1)Найти координаты точек пересечения прямых с осями координат
а)x−y = −1 преобразуем выражение в уравнение функции:
-у= -1-х
у=1+х
График пересекает ось Ох при у=0.
у=0
0=1+х
-х=1
х= -1
Координаты точки пересечения графиком оси Ох (-1; 0)
График пересекает ось Оу при х=0.
х=0
у=1+х
у=1+0
у=1
Координаты точки пересечения графиком оси Оу (0; 1)
б)2x + y = 4 преобразуем выражение в уравнение функции:
у=4-2х
График пересекает ось Ох при у=0.
у=0
0=4-2х
2х=4
х= 2
Координаты точки пересечения графиком оси Ох (2; 0)
График пересекает ось Оу при х=0.
х=0
у=4-2х
у=4-0
у=4
Координаты точки пересечения графиком оси Оу (0; 4)
2)Найти точку пересечения этих прямых друг с другом.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у=1+х у=4-2х
Таблицы:
х -1 0 1 х -1 0 1
у 0 1 2 у 6 4 2
Согласно графика, координаты точки пересечения (1; 2)
(Значения таблиц подтверждают это).
Пишите если что то непонятно