Произведение чисел, переменных и их степеней называется одночленом, например,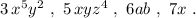 
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
,
.
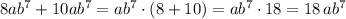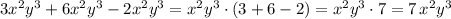Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
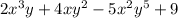не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов, но в результате всё равно получим многочлен:
.
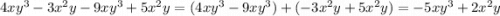x1=1/4[-7-11]=-18/4=-4.5
x2= 1/4[-7+11]=2
3x²-18x=3x(x-6)=0 x1=0 x2=6
100x²=16 x²=0.16 x1=0.4 x2=-0.4
x²-16x+63=0 D=16²-4*63=256-252=4 √4=2
x1=1/2[16-2]=7
x2=1/2[16+2]=9
2.
2(a+b)=20 a+b=10 b=10-a
ab=24 a(10-a)=10a-a²=24 a²-10a+24=0 по теореме Виета корни
6 и 4. a=6 b=4 или a=4 b=6
3. x²+px-18=0 подставим х=-9
81-9p-18=0 9p=81-18=63 p=63/9=7
второй корень. Произведение корней = -18 -9*x2=-18
второй корень = 18/9=2