1) D = 25 -4(2×20)=25-160= -135
Значит действительных корней нет
2) по теореме не знаю какого автора
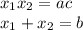
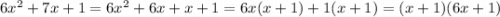
получаем разложение на множители, из которых быстро находим корни
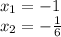
3) Обратная теорема Виета
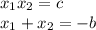
подходящие нам числа это -8 и -3, при умножении дают 24, а при складывании -11
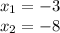
4) Воспользуемся формулой выше
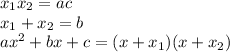
(если у нас коэффициент а>1 сначала нужно разложить bx как сумму х1 и х2 и только потом выносить общий множитель, пример ниже)
6 × (-3) = -18
6-3=3
(х+6)(х-3)
5)
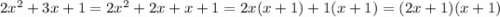
Если мы для разложения хотим воспользоваться обратной теоремой Виета, нам нужно найти корни уравнения, а потом записать их в таком виде
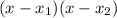
где х1 и х2 это корни уравнения
пример:
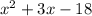
находим корни
-6 × 3 = -18 (с)
-6 +3= -3 (-b)
получаем
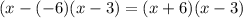
Дано:
- арифметическая прогрессия.
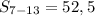
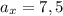
Найти: 
Решение.
1) 
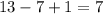- количество членов с седьмого по тринадцатый.
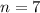
2) 
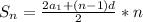формула суммы 
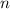членов арифметической прогрессии
Для суммы членов с седьмого по тринадцатый первым
членом будет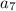 
.
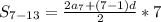
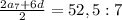
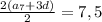
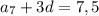
3) По формуле общего члена арифметической прогрессии
выразим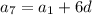 
.
Подставим в уравнение 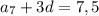и получим:
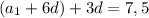
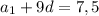
4) По условию один из членов данной прогрессии с номером
равен 7,5.
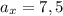иначе
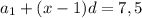
5) Очевидно, что два уравнения
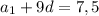и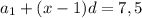
имеют равные правые части 7,5 = 7,5 , а это значит, что
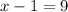
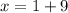
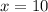
10-й член данной прогрессии равен 7,5.
ответ: 10.
4х-9у=39 I *3
-12х+11у=-69
12х-27у=117
-12х+11у=-69
сложим
-16у=48
у=-3
х=(39+9у)/4=(39-27)/4=3
(3;-3)