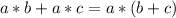(k+1)*к+2(к+1)
У Вас одинаковая скобка (к+1), я ее выделил жирным шрифтом.
Ее мы вынесем за скобку. Эдак, скобку за скобку. Чтобы понять, что останется внутри второй скобки, надо каждое слагаемое разделить на ту скобку, которую Вы вынесли, т.е. на (к+1)
Итак, (к+1)*к/(к+1)=к, а от второго слагаемого останется 2*(к+1)/(к+1)=2, все, что попадет во вторые скобки, я подчеркнул.
Итак, (k+1)*к +2(к+1)=(к+1)*(к+2)
Изменим порядок следования, получим именно то, что Вам надо.
(k+1)*к+2(к+1)=(к+2)(к+1)*
1). что-то не то с условием: из четырех чисел нельзя составить пятизначное число, не имеющие в составе повторяющихся цифр.
2). по признаку делимости на 5: чтобы число делилось на 5, надо, чтоб оно оканчивалось на 0 или 5. Т.к. данные цифры не используются, то числа, делящиеся на 5 составить нельзя.
по признаку делимости на 4: чтобы число делилось на 4, надо, чтоб число составленное из двух последних цифр в том же порядке делилось на 4. из данных цифр можно составить только числа оканчивающиеся на 24, 72, 32.
разберем вариант с 24. тогда с первой и второй цифрами числа так: т.к. цифры не повторяются 2 и 4 использовать нельзя. тогда на первое место в числе можно поставить любую из двух оставшихся цифр (таких 2), а на второе место уже оставшуюся цифру...в результате количество требующихся чисел 2*1=2.
аналогично получим 2 числа оканчивающиеся на 32 и 2 числа оканчивающиеся на 72.
ответ: а) 6 чисел. б) ни одного
3). т.к. учебники алгебры могут стоять только рядом, то возьмем их как один объект, тогда объектов, которые надо расставить у нас 4 (причем 3 из них одного вида - учебники геометрии (я так понимаю нет разницы какой из них будет стоять раньше, какой позже)). существует формула для перестановок с повторениями:

где n - общее кол-во объектов, а и т.д. - кол-во объектов каждого вида
получаем
4). Чисел которые начинаются с 2 - можно составить два. чисел, где 2 стоит на втором месте - тоже два, где на третьем - два. аналогично для 4 и 6.
теперь найдем сумму всех таких чисел: (2*100+2*10+2)*2+(4*100+4*10+4)*2+(6*100+6*10+6)*2
Как можно заметить, тут есть два слагаемых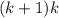 и
и 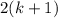 с двумя одинаковыми множителям - скобками
с двумя одинаковыми множителям - скобками 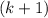 . Вынесем их за скобку.
. Вынесем их за скобку.
Это делается по аналогии с вынесением переменной за скобки, только вместо переменной тут выносится целая скобка.
Теория:
Распределительный закон умножения относительно сложения: