
2 sin x – cos x =1
2sin x/2 * cos x/2 – cos² x/2 +sin² x/2 = sin² x/2 + cos² x/2
2sin x/2 * cos x/2 – 2cos² x/2 = 0
2cos x/2 * (sin x/2 – cos x/2) =0
cos x/2 * (sin x/2 – cos x/2) =0
cos x/2 = 0 или sin x/2 – cos x/2 = 0
cos x/2 = 0;
x/2 = π/2 + πk;
x = π + 2πk; k Є Z;
sin x/2 – cos x/2 = 0 – однородное уравнение первой степени.
Делим обе его части на cos x/2 (cos x/2≠ 0, так как,
если cos x/2 = 0, sin x/2 – 0 = 0 => sin x/2 = 0, что противоречит тождеству sin² x/2 + cos² x/2 = 1).
Получим tg x/2 – 1 = 0;
tg x/2 = 1;
x/2 = π/4 + πn;
x = π/2 + 2πn; n Є Z.
1) x = π + 2πk; k Є Z;
y = π/2 + π + 2πk; k Є Z;
y = π + 2πk; k Є Z;
(π + 2πk; k Є Z; π + 2πk; k Є Z;)
2) x = π/2 + 2πn; n Є Z.
y = π/2 + π/2 + 2πn; n Є Z.
y = π + 2πn; n Є Z.
(π + 2πk; k Є Z; π + 2πk; k Є Z)
ответ: (π + 2πk; k Є Z; π + 2πk; k Є Z) ;
(π + 2πk; k Є Z; π + 2πk; k Є Z)
A) х>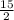
Б)0>x
Объяснение:
а) 9x+15<3(7x-5) "Идет метод фонтанчика умножаем 3 на 7x минус 3 умножить на 5"
9x+15<3*7x-3*5
9x+15<21x-15 "Дальше можно сократить цифры находящиеся перед X"
9 и 21 - Общий множитель 3 "Делим их на 3"
3 и 7 - убираем обратно
3х+15<7х-15 "ДАЛЬШЕ ПЕРЕНОСИМ иксы к иксам числа к числам
3x-7x<-15-15
-4x<-30
x=30/-4
х>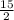
б) 5(4x-2)>11x-10 "Идет метод фонтанчика умножаем 5 на 4x минус 5 умножить на 2"
20x-10>11x-10 "Дальше нужно убрать -10 потому что он и там и там одинаковый"
20x>11x
x>0
Удачи в учёбе