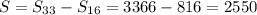Пусть начальная скорость велосипедиста х, тогда скорость с которой он возвращался х+3. Время, которое потратил велосипедист на преодоление расстояния от А до Б равно 30/х, а на расстояние от Б до А - 30/(х+3). Известно, что на возвращение велосипедист потратил на 30 минут меньше времени (что составляет 0,5 часа), значит можно записать уравнение: 30/х-30/(х+3)=0,5 30*(х+3)-30*х=0,5х(х+3) 30х+90-30х=0,5х²+1,5х 0,5х²+1,5х-90=0 D=1,5²-4*0,5*(-90)=2,25+180=182,25 x₁=(-1,5-13,5)/(2*0,5)=-15/1=-15 x₂=(-1,5+13,5)/(2*0,5)=12/1=12 Так как скорость не может быть отрицательной выбираем ответ 12 км/ч
1) Разность арифметической прогрессии: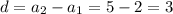
. Тогда по формуле n-го члена арифметической прогрессии, найдем четырнадцатый член:
2) Пятый член: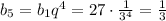
Сумма четырех первых членов геометрической прогрессии:
3) Знаменатель прогрессии:
Сумма бесконечно убывающей геометрической прогрессии:
4) Здесь в условии опечатка, скорее всего d=-0.5, а если так как есть то задача решения не имеет.
ответ: 7
5)
- геометрическая прогрессии
6) 6; 12; .... ; 96; 102; 108; .... ;198 - последовательность чисел, кратных 6.
Посчитаем сколько таких чисел:
Сумма первых 33 членов а.п.:
Нам нужно найти сумму всех натуральных чисел превышающих 100 и меньших 200 , которые кратны 6
, значит найдем сумму не превышающих 100 и отнимем от суммы не превышающих 200
Искомая сумма: