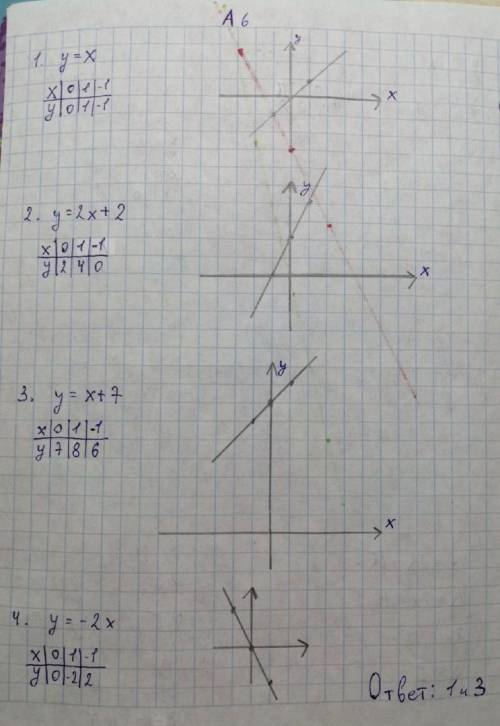
А6 - 1,3
В1 - (20;20)
В2 - (2;0)
С1 - 2
С2 - (фотка)
Объяснение:
А6. решение на фото
В1. чтобы найти координату пересечения графиков функции нужно их прировнять
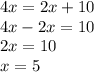
Найдём Y если подставим полученное значение Х в функцию (можно подставить в любую)
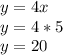
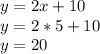
Точка пересечения графиков функции имеет следующие координаты (20;20)
В.2
Ось абсцисс - это ось ОХ
Чтобы найти координату пересечение графика функции с осью абсцисс
Нужно прировнять Y к 0, так как нам нужно пересечение графика функции с осью абсцисс
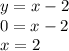
Точка пересечение графика функции с осью абсцисс имеет следующие координаты (2;0)
С.1
Мы имеем функцию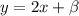 
и точку с координатами (0;2)
Чтобы найти b мы подставим координаты точки в функцию
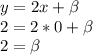
С.2 решение на фото
( 
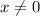так как при делении любого выражения на 0 получается неопределённое выражение)
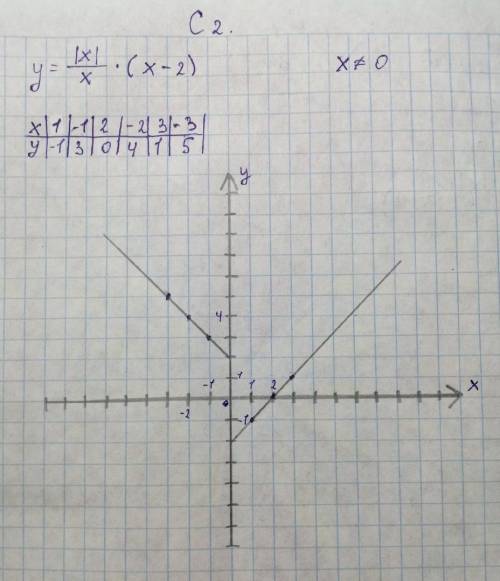
1) f(-3,5) = -0.5; f(-2,5) = 2; f(-1) = 0; f(2) = -1.
Здесь последовательно находим абсциссы х=-0,5; х=-2,5; х=-1; х=2, проводим прямую, параллельно оси оу до точки пересечения с графиком и называем, чему в этой точке равна ордината.
2) f(x)=-2,5, если х = 5 ; f(x)=-2, если х=3,5;
f(x)=0, если х=-3, х=-1, х=1,5;
f(x)=2, если х=0; х=-1,5, х=-2,5.
Здесь наоборот, по известной ординате, у=-2,5; у=-2; у=0; у=2 находим абсциссу х, их может быть несколько, т.к. прямая, параллельная оси ох пересекает график в нескольких точках, опускаем из этих точек перпендикуляры на ось ох и читаем ответы
3) Е(у) = [-2,5; 3]- это те значения, которые пробегает у. самое маленькое у=-2,5, самое большое у=3.
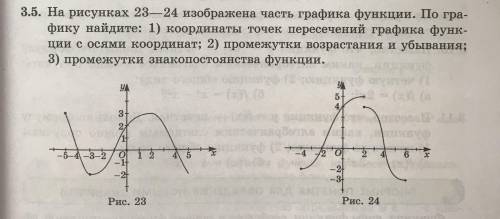
Рис.23:
1) С осью х: (-4;0); (-1;0); (4;0)
С осью у: (0;2)
2) Возрастание: [-3:2]
Убывание: [-5;-3], [2;5]
3) Положительна: [-5;-4), (-1;4)
Отрицательна: (-4;-1), (4;5]
Рис.24:
1) С осью х: (-2;0);(4;0)
С осью у: (0;4)
2) Возрастание: [-4:2)
Убывание: (2;6]
3) Положительна: (-2;4)
Отрицательна: [-4;-2), (4;6]
Объяснение: