Реши систему графическим
ответь на вопросы письменно:
1)Как решается система графическим
2)Почему координаты точек пересечения являются решением системы уравнений?
3)Как записывается решение системы уравнений, если она решается графическим
4)От чего зависит количество решений системы уравнений при графическом решения?
5)Сколько точек имеют графики, если система имеет три решения?
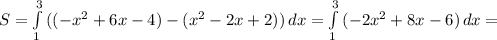
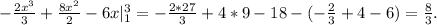
Пусть х дм - длина стороны первого квадрата; (ОДЗ: x>0)
у дм - длина стороны второго квадрата, (ОДЗ: y>0)
тогда
х² дм² - площадь первого квадрата;
у² дм² - площадь второго квадрата.
По условию сумма их площадей равна 25 дм², получаем первое уравнение:
x² + y² = 25
По условию произведение длин сторон данных квадратов равно 12дм², получаем второе уравнение:
xy = 12
Решаем систему:
{x²+y² = 25
{xy = 12
Второе уравнение умножим на 2.
{x²+y² = 25
{2xy = 24
Теперь сложим:
x²+ 2xy +y² = 25+24
(x+y)² = 49
1) x+y = √49 = - 7 < 0 не удовлетворяют ОДЗ.
2) x+y = √49 = 7
Берем уравнение
x+y = 7
и второе уравнение xy = 12 и решаем систему:
{x+y=7
{xy = 12
Из первого уравнения выразим у и подставим во второе:
y=7-x
x·(7-x) = 12
7х-x²=12
x²-7x+12 = 0
D=49-4·1·12 = 49-48=1 = 1²
x₁=(7-1)/2=6/2=3
x₂=(7+1)/2=8/2=4
Найдем у:
y₁=7-3=4
y₂=7-4=3
ответ: (3дм; 4дм) или (4дм; 3дм)