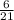Есть два решения этой задачи - стандартное и на сообразительность.
Начну со второго. Учитывая, что расстояние между домами равно сумме высот дома и фонаря, нужного результата мы добьемся, если рассыпем зёрна на расстоянии 6 метров от дома. Тогда катеты левого прямоугольного треугольника равны 8 и 6 метров, правого - 6 и 14-6=8 метров. То есть эти треугольники равны, а тогда у них равны гипотенузы, чего и нужно было добиться.
Первый Если расстояние от первого дома равно x, то квадрат гипотенузы левого треугольника равен 8²+x², а квадрат гипотенузы правого треугольника равен 6²+(14-x)²; а поскольку гипотенузы по условию должны быть равны, получаем уравнение
64+x²=36+196-28x+x²; 28x=168; x=6
ответ: 6 метров
/7х-9/+5*/9-7х/=0
/7х-9/+/45-35х/=0
7х+9+45+35х=0
42х+54=0
42х=-54
х=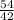
х=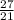
х=1