Question

Знатоки алгебры ОЧЕНЬ По графику на фото

a) Запишите область определения функции.

b) Найдите множество значений функции.

c) Определите промежутки знакопостоянства функции;

d) Определите максимальное значение функции на области определения;

e) Определите четность функции.

​

Answer 1

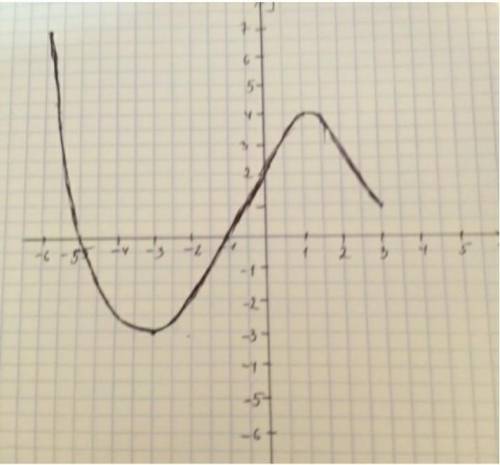
Описание функции по ее графику.

Объяснение:

a)

D(f)=[-6;3]

b)

E(f)=[-3;7]

c)

f(x)>0,

если х€[-6;-5)обьед.(-1; 3]

f(x)<0,

если х€(-5; -1)

d)

Максимального значения функция

достигает в точке х=-6.

fmax(-6)=7

В точке х=1 функция достигает ло

кального максимума f(1)=4, но полу

ченное значение не будет max во

всей обрасти определения. Макси

мального значения функция дости

гает в точке х=-6, которая лежит на

границе области определения.

е) Функция не является ни четной

ни нечетной ( функция общего вида).

Если функция четная, то график

симмметричен относительно ОУ.

Если функция нечетная, то график

симметричен относительно точки

начала отсчета (0; 0).

На чертеже график не имеет сим

метрии ==> имеем функцию обще

го вида.

Answer 2

$a)\ \ OOF:\ x\in D(y)=[-6\, ;\, 3\ ]\\\\b)\ \ MZF:\ y\in E(y)=[-3\, ;\, 7\ ]\\\\c)\ \ y0\ ,\ esli\ \ x\in [-6\, ;\, -5)\cup (-1\, ;\, 3\ ]\\\\{}\ \ \ \ y$

e)  функция не является ни чётной, ни нечётной, так как нет симметрии ни относительно оси ОУ, ни относительно точки (0;0) .