
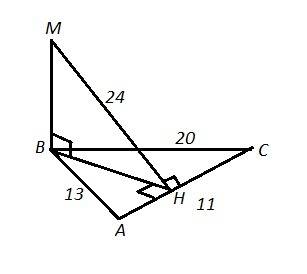
ΔАВС , АВ=13 , АС=11 , ВС=20
Наименьший угол в треугольнике лежит против наименьшей стороны,
то есть ∠В - наименьший, сторона АС=11 - наименьшая.
ВМ ⊥ пл. АВС ⇒ ВМ ⊥ любой прямой , лежащей в пл. АВС, в том числе и высоте треугольника ВН, ВН ⊥ АС.
Тогда по теореме о трёх перпендикулярах МН⊥АС (ВН - проекция МН на пл. АВС) ⇒ МН=24.
Найдём ВН , используя две формулы нахождения площади ΔАВС.
S(ABC)=1/2*АС*ВН ⇒ ВН=2S/АС .
Полупериметр р=1/2*(11+13+20)=22 ,
S=√p*(p-a)(p-b)(p-c)=√(22*11*9*2)=66 .
ВН=2*66/11=12 .
ΔВМН: ∠МВН=90° , ВМ=√(МН²-ВН²)=√(24²-12²)=√432=12√3
Объяснение:
Постройте график функции y= 2x-5.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -7 -5 -3
Пользуясь графиком, найдите:
1) значение функции,если значение аргумента равно 3.
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=3
у=2*3-5=1 при х=3 у=1
2) значение аргумента,если значение функции равно -1.
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -1
-1=2х-5
-2х= -5+1
-2х= -4
х=2
В решении.
Объяснение:
1) -2х+19=5х-16
-2х-5х= -16-19
-7х= -35
х= -35/-7
х=5
(5; 1)
2) 8х-25 =3х+20
8х-3х=20+25
5х=45
х=45/5
х=9
(9; 0)
3) 6-у=3(3у-8)
6-у=9у-24
-у-9у= -24-6
-10у= -30
у= -30/-10
у=3
(5; 3)
4) 5(у+1,2)=7у+4
5у+6=7у+4
5у-7у=4-6
-2у= -2
у= -2/-2
у=1
(1; 1)
5) 4(х-3)-16=5(х-5)
4х-12-16=5х-25
4х-5х= -25+28
-х=3
х=3/-1
х= -3
(-3; 3)
6) 3х-17=8х+18
3х-8х=18+17
-5х=35
х=35/-5
х= -7
(-7; 0)
7) 11-5у=12-6у
-5у+6у=12-11
у=1
(-3; 1)
8) 4у+(11,8-у)=3,8-5у
4у+11,8-у=3,8-5у
3у+5у=3,8-11,8
8у= -8
у= -8/8
у= -1
(1; -1)
9) 3х+16=8х-9
3х-8х= -9-16
-5х= -25
х= -25/-5
х=5
(5; 1).
(Соединять точки нужно в порядке вычислений, получится вытянуто-приплюснутая буква М)