
Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение:
1)
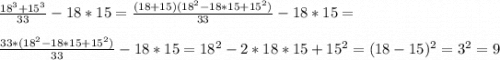
2)
2x³-54=2*(x³-27)=2*(x³-3³)=2*(x-3)(x²-3x+9)
3) а
(3х-4)²+(2х-4)(2х+4)+65х=
9х²-24х+16+4х²-16+65х=
13х²+41х=x(13x+41)
b)
при x=-3
x*(13x+41)= -3*(13*(-3)+41)=-3*(-39+41)=-3*(-2)=-6
4)
х-первое число
у-второе число
х²-у²=52}
х+у=26 }
(x-y)(x+y)=52 (1)
(x+y)=26 подставим в (1) ,получим
(х-у)*26=52} сократим на 26
х+у=26 }
x-y=2 }
x+y=26 } сложим левые и правые части
----------------------------------------
х+х-у+у=26+2
2х=28
х=28:2
х=14 подставим в x-y=2 получим
14-у=2
у=12
ответ: числа 12 и 14.
Мы знаем, что на первом месте в записи координата точки пишется x, а на втором y, значит, чтобы функция проходила через эту точку, нужно подставить эти значения.
1=1^3-12*1+12
1=1-12+12
1=1