x²+y²-8x+6y=0
x²-8x+16+y²+6y+9-25=0
x²-8x+16+y²+6y+9=25
(x-4)²+(y+3)²=25
координаты центра:
( 4 ; -3)
радиус:
5
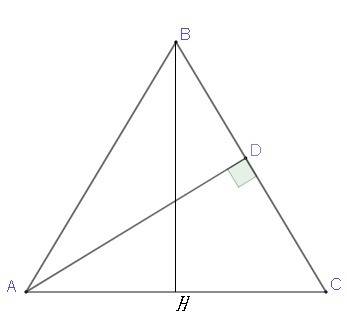
Дано: ABC - равнобедренный треугольник; AC = 12 см; AD = 9.6 см; AB=BC.
Найти: Рabc.
Из прямоугольного треугольника ADC по теореме Пифагора найдем CD
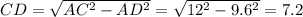 см.
см.
Пусть 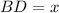 , тогда
, тогда 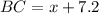 .
.
Рассмотрим прямоугольный треугольник BHC найдем высоту BH к стороне основания AC; AH=CH=AC/2=6 см.
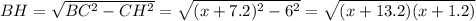
Площадь равнобедренного треугольника равна 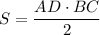 , с другой стороны
, с другой стороны 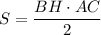
Приравнивая площади, получим AD * BC = BH * AC.
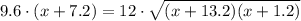
После возведения в квадрат обе части уравнения и упрощений с подобными членами вы должны получить следующее квадратное уравнение
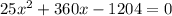
Корни которого:  - не удовлетворяет условию
- не удовлетворяет условию
 см
см
Тогда 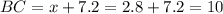 см
см
Pabc = AB + BC + AC = 10 + 10 + 12 = 32 см
ответ: 32 см.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
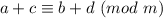
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
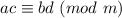
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
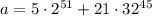
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 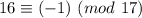 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 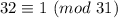 , получаем
, получаем
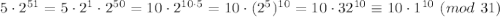
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
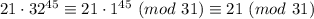
Остаток 21, чудесно. Выполняем последний шаг.
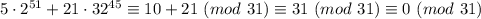
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Надо выделить полные квадраты .
Центр окружности в точке (4;-3) , радиус R=5 .