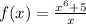
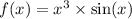

Для начала вспомним графики функций y = [x] и y = {x}:
Первый представляет собой целую часть числа x. Например
[3,2] = [3 + 0,2] = 3
[-4,5] = [-5 + 0,5] = -5
График такой функции прикреплён во вложении.
Второй представляет собой дробную часть аргумента x, то есть y = x - [x]. Например
{3,2} = 3,2 - 3 = 0,2
{-4,5} = -4,5 - (-5) = 0,5
График также во вложении.
Теперь перейдём к заданию:
При выполнении используются правила геометрических преобразований.
1) y = [x + 1]
Берём за основу график функции y = [x] и смещаем его влево вдоль оси OX на 1.
2) y = [x] + 2
Берём за основу график функции y = [x] и смещаем его вверх вдоль оси OY на 2 единицы.
3) y = {x - 1/3}
Берём за основу график функции y = {x} и смещаем его вправо вдоль оси OX на 1/3 единицы.
4) y = {x} + 1
Берём за основу график функции y = {x} и смещаем его вверх вдоль оси OY на 1.
5) y = [3x + 1]
Сначала рассмотрим график y = [x + 1]. Он уже построен в пункте 1)Но в требуемом графике "3x", поэтому нужно к графиком y = [x + 1] применить ещё одно преобразование:Сначала рассмотрим график y = [3x]. По правилу геометрического преобразования, чтобы построить этот график, надо график функции y = [x] сжать в 3 раза вдоль оси OX.Так как в нашем случае функции имеет вид y = [x + 1], то и сжимать в три раза будем именно её.Таким образом, чтобы построить график функции y = [3x + 1] надо:
1) Взять за основу график функции y = [x] и сместить его влево вдоль оси OX на 1.
2) Полученный график сжать вдоль оси OX в 3 раза.
Все графики во вложении
![Построить график функции: 1) у=[х+1]; 2) у=[х]+2; 3) у={х-1/3}; 4) у={х}+1; 5) у=[3х+1]. с объяснени](/tpl/images/0968/4679/f1000.jpg)
![Построить график функции: 1) у=[х+1]; 2) у=[х]+2; 3) у={х-1/3}; 4) у={х}+1; 5) у=[3х+1]. с объяснени](/tpl/images/0968/4679/62280.jpg)
1) Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя (в одной из групп общего множителя может не быть).
2) Вынесение полученного общего для всех групп множителя за скобки.
Примеры.
\[1)ax + 7a - 3x - 21 = \]
Группируем первое слагаемое со вторым, третье — с четвертым.
Лучше при группировке между скобками всегда ставить знак «+»:
\[ = (ax + 7a) + ( - 3x - 21) = \]
Из первых скобок выносим общий множитель a, из вторых — -3. При вынесении «-» за скобки все знаки в скобках меняем на противоположные:
\[ = a(x + 7) - 3(x + 7) = \]
Общий множитель (x+7) выносим за скобки:
\[ = (x + 7)(a - 3)\]
Группировать можно было иначе: первое слагаемое — с третьим, второе — с четвертым:
\[ax + 7a - 3x - 21 = (ax - 3x) + (7a - 21) = \]
Из первых скобок выносим общий множитель x, из вторых — 7:
\[ = x(a - 3) + 7(a - 3) = \]
Общий множитель (a-3) выносим за скобки:
\[ = (a - 3)(x + 7)\]
При любом группировки ответ получается одинаковый (от перестановки мест множителей произведение не меняется).
\[2)4x - xy - 4 + y = \]
Группируем первое слагаемое со вторым, третье — с четвертым:
Область определения функции и в а) и в в) симметрична относительно начала отсчета.
найдем f(-x)=((-x)⁶+5)/(-x)=-(x⁶+5)/x=-f(x)
f(x)=(x⁶+5)/x- нечетная функция.
в) f(-x)=(-х)³*sin(-x)=-(х)³*(-sin(x))=(х)³*(sin(x))=f(x)
f(x)=х³*(sin(x))- четная функция.