Можно сделать систему:
3-x/4<=2
3-x/4>-1
-x/4<=-1
-x/4>-4
-x<=-1*4
-x>-16
x>=4
x<16
ответ: x принадлежит от [4;16)
a ∈ (16/17; 2)
Объяснение:
(2 – a)x² – 3ax + 2a = 0
При a = 2 квадратное уравнение вырождается в линейное, а следовательно имеет единственный корень, что не соответствует условию задачи, поэтому 2 – a ≠ 0 и a ≠ 2.
У квадратного уравнения имеется два различных корня тогда и только тогда, когда дискриминант строго больше нуля.
D = (–3a)² – 4·(2 – a)·2a = 9a² – 16a + 8a² = 17a² – 16a = a·(17a – 16)
Корнями уравнения a·(17a – 16) = 0 являются числа a₁ = 0 и a₂ = 16/17, и поэтому D = a·(17a – 16) > 0 при a < 0 или a > 16/17.
Разделим обе части исходного уравнения на (2 – a), чтобы получить приведенное квадратное уравнение:
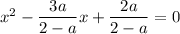
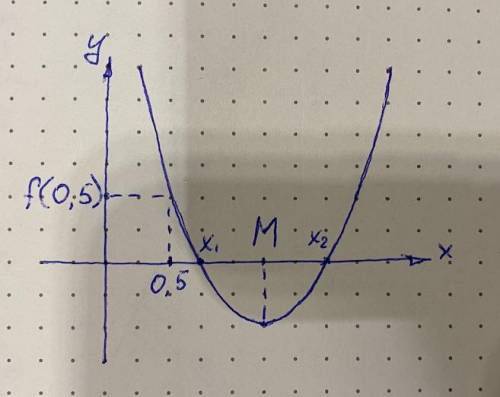
Полученное уравнение задает параболу, причем ветви параболы направлены вверх. Одновременно оба корня уравнения будут лежать с одной стороны от точки x = 0.5, когда f(0.5) > 0 (см. рисунок):
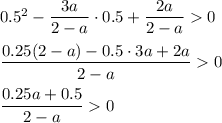
"Корнями" являются a₁ = –2 и a₂ = 2, неравенство выполняется при –2 < a < 2.
По теореме Виета значение 3a / (2 – a) равно сумме корней уравнения. Тогда M = 3a / (4 – 2a) является арифметическим средним корней и лежит ровно посередине между ними. Оба корня будут лежать справа от x = 0.5, когда их среднее M > 0.5 (см. рисунок):
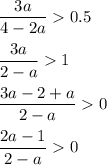
"Корнями" являются a₁ = 0.5 и a₂ = 2, неравенство выполняется при 0.5 < a < 2.
Таким образом, корни уравнения (2 – a)x² – 3ax + 2a = 0 являются действительными и оба больше 0.5 при одновременном выполнении системы из трех условий:
1. дискриминант строго больше нуля ⇒ a ∈ (–∞; 0) ∪ (16/17; +∞),
2. для приведенного уравнения справедливо f(0.5) > 0 ⇒ a ∈ (–2; 2),
3. среднее значение корней приведенного квадратного уравнения больше 0.5 ⇒ a ∈ (0.5; 2).
Пересекая полученные интервалы, получаем ответ: a ∈ (16/17; 2).
Ну воь смотри у тебя там есть такая табличка с надписью"существуют учебники по математике и ты нажимаешь на неё и зажимаешь правую кдавишу на мышке и переносишь её в ту табличку которая должна давать правильное утверждение зелёной таблицы я так думаю это зеленая соответствует той коричневой с надписью"общие утверждения если ещё там есть такое задание то тогда так же перетаскивай в нужную табличку ту табличку"
Объяснение:
Надеюсь я толком объяснила если все же не правильно пиши в коментарях я отвечу
отнимаем от каждой части 3
-4<-x/4<(или равно)-1
умножаем каждую часть на 4
-16<-x<(или равно)-4
делим на -1 приэтом меняем знаки на противоположенные
16>x>(или РАвно)4