Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
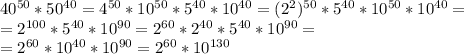
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
при х<-1 выражение примет вид
4/( -x-1) - 2 >= - x +1
при -1<х<1 выражение примет вид
4/( x+1) - 2 >= - x +1
при х>=1 выражение примет вид
4/( x+1) - 2 >= x - 1
4/( -x-1) - 2 >= - x +1 <=> 4 - 2(-x-1)>=(-x+1)(-x-1) <=>4+2x+2>=x^2-1 <=> x^2-2x-7<=0
D=8 1-(корень из 8 ) <= x <= 1+(корень из 8) но т.к. x<-1 то 1-(корень из 8 ) <= x < -1
4/( x+1) - 2 >= - x +1 <=>4-2x-2>= - x^2+1 <=>x^2-2x+1>=0 <=> (x-1)^2>=0 при всех х , но мы рассматриваем -1<х<1
4/( x+1) - 2 >= x - 1 <=>4-2х-2>=x^2-1<=>x^2+2x-3<=0
D=4+12=4^2 (-2-4)/2<=x<=(-2+4)/2 -3<=x<=1 но т к мы рассматриваем при х>=1 то х=1
ответ 1-(корень из 8 ) <= x < -1
-1<х<=1