y=0,5x²
у=х²
у=4х²
Все три графика - параболы с вершиной в точке (0; 0)
Коэффициент при х показывает степень сжатия/расширения графика. Чем меньше коэффициент, тем "шире" парабола, чем больше коэффициент, тем "уже" парабола.
Таблицы значений:
у=0,5x² у=х² у=4х²
х у х у х у
-4 8 -4 16 -4 64
-2 2 -2 4 -2 16
0 0 0 0 0 0
2 2 2 4 2 16
4 8 4 16 4 64
График в файле.
Объяснение:
y=-6x²-3x
функция квадратичная вида ax²+bx+c - значит парабола
аргумент а - отрицательный, значит ветви параболы направлены вниз.
с=0, значит одна из ветвей пересекает ось Оу в точке с координатой у=0, если так, то и ось Ох она пересекает с координатой х=0, т.е. ветвь параболы проходит через начало координат.
находим точки пересечения с осью Ох
-6х²-3х=0
-3х(2х+1)=0
х1=0
2х+1=0
2х=-1
х2=-1/2
находим вершину параболы
х=-b/(2a)
x=3/-12=-1/4
y=-6*(-1/4)²-3*(-1/4)=3/8
(-1/4;3/8) - координаты вершины
Строим график.
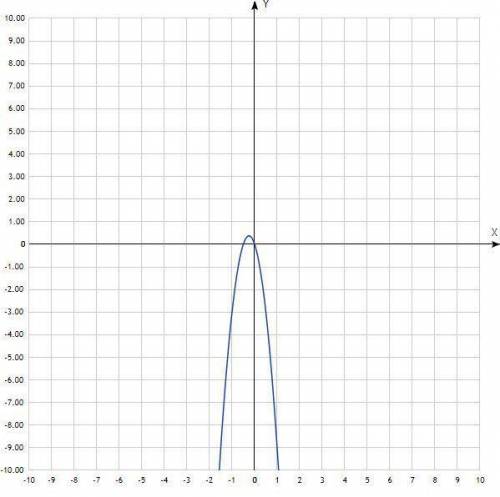
нужно построить в одной системе координат графики функций у = х2 и
у = 2х + 3 . Они пересекаются в двух точках А(- 1; 1) и В(3; 9). Корнями уравнения служат абсциссы точек А и В, значит, х1 = -1, х2 = 3.
я файл вложила правда рисунок не очень ну ты построй и поймешь х²=2х+3 х²-2х-3 Построим график функции у = х2 - 2х - 3
1) Имеем а = 1, b = -2, х=-b/2a=1, у = f(1) = I2 - 2 - 3 = - 4. Значит, вершиной параболы служит точка (1;- 4), а осью параболы — прямая х = 1.
2) Возьмем на оси х две точки, симметричные относительно оси параболы: точки х = -1 и х =3. Имеем /(-1) = /(3) = 0; отметим в координатной плоскости точки (-1; 0) и (3; 0).
3) Через точки (-1; 0), (1; -4), (3; 0) проводим параболу (рис.1).Корнями уравнения
х2 - 2х - 3 = 0 являются абсциссы точек пересечения параболы с осью х; находим
x1= -1,
x2 = 3
рисовать не буду нет времени
его можно решить Решите графически уравнение : х²=2х+3">