1 Данная задача решается аналитически, поэтому можно вовсе не рисовать графики прямой и параболы. Часто это дает большой плюс в решении примера, так как в задаче могут быть даны такие функции, что их проще и быстрее не нарисовать. 2 Согласно учебникам по алгебре парабола задается функцией вида f(x)=ax^2+bx+c, где a,b,c – это вещественные числа, притом коэффициент a отличен он нуля. Функция g(x)=kx+h, где k,h – это вещественные числа, определяет прямую на плоскости. 3 Точка пересечения прямой и параболы – это общая точка обеих кривых, поэтому в ней функции примут одинаковые значение, то есть f(x)=g(x). Данное утверждение позволяет записать уравнение: ax^2+bx+c=kx+h, которое даст возможность найти множество точек пересечения. 4 В уравнении ax^2+bx+c=kx+h необходимо перенести все слагаемые в левую часть и привести подобные: ax^2+(b-k)x+c-h=0. Теперь остается решить полученное квадратноеуравнение. 5 Все найденные "иксы" – это еще не ответ на задачу, так как точку на плоскости характеризуют два вещественных числа (x,y). Для полного завершения решения необходимо вычислить соответствующие "игрики". Для этого нужно подставить "иксы" либо в функцию f(x), либо в функцию g(x), ведь для точки пересечения верно: y=f(x)=g(x). После этого вы найдете все общие точки параболы и прямой. 6 Для закрепления материала очень важно рассмотреть решение на примере. Пусть парабола задается функцией f(x)=x^2-3x+3, а прямая – g(x)=2x-3. Составьте уравнение f(x)=g(x), то есть x^2-3x+3=2x-3. Перенося все слагаемые в левую часть, и приводя подобные, получите: x^2-5x+6=0. Корни данного квадратного уравнения: x1=2, x2=3. Теперь найдите соответствующие "игрики": y1=g(x1)=1, y2=g(x2)=3. Таким образом, найдены все точки пересечения: (2,1) и (3,3).
(1) х+у=5 и х-у=1 у=5-х и у=х-1 а) Строим график функции у=5-х х=1, у=4 х=2, у=3 Отметь точки (1;4) и (2;3) и проведи через них линию на всю плоскость координат б) Строим график функции у=х-1 х=1, у=0 х=2, у=1 Отметь точки (1;0) и (2;1) и проведи через них линию на всю плоскость координат Отметь точку пересечения - это и есть ответ ответ: х=3, у=2
(2) 2х+3у=13 и 3х-у=3 у=(13-2х) /3 и у=3х-3 а) Строим график функции у=(13-2х) /3 х=2, у=3 х=5, у=1 Отметь точки (2;3) и (5;1) и проведи через них линию на всю плоскость координат б) Строим график функции у=3х-3 х=1, у=0 х=2, у=3 Отметь точки (1;0) и (2;3) и проведи через них линию на всю плоскость координат Отметь точку пересечения - это и есть ответ ответ: х=2, у=3
Объяснение:
1.
a) 12, 36,12, 8, 24, 16
Упорядочим ряд:
8, 12, 12, 16, 24, 36
Ср. арифметическое: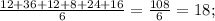
Размах: 36-8=28;
Мода: 12.
б) -2, 45 ,-8, 45, 35
Упорядочим ряд:
-8, -2, 35, 45, 45
Ср. арифметическое: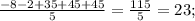
Размах: 45-(-8)=45+8=53;
Мода: 45.
2.
a) 25, 43, 44, 51, 55, 67, 72
Медиана: 51.
б) 3, 12, 24, 32, 43, 54
Медиана: