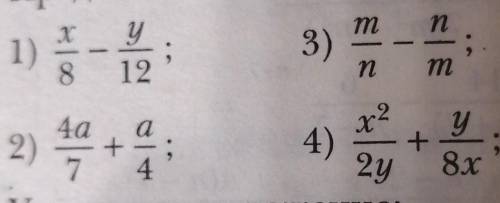
Первую ещё не придумала, а вот вторая:
Чтобы найти вероятность того, что точка,брошенная в круг, попадёт в треугольник, надо найти отношение площади правильного треугольника к площади окружности
S(треуг)=(а:2*корень(3))/ S 4
S(окруж)=Pі *r^2
Мы знаем связь между стороной правильного треугольника и радиусом описаной окружности:
r=a/корень3
Тогда, вероятность = S(треуг)/ S(окруж)= ((а:2*корень(3))/ S 4) / (Pі *r^2) = ((а:2*корень(3))/ S 4) * (Pі *а^2) /3=(3*корень3)/ 4Pі
Если надо, можно примерно вищитать:
(3*корень3)/ 4Pі = 3*1,73/4*3,14=5,19/12,56=0,41
ответ:0,41

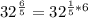
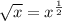
![\sqrt[3]{x} =x^{\frac{1}{3}}](/tpl/images/0503/0859/f093d.png)
![32^{ \frac{1}{5}} =\sqrt[5]{32}](/tpl/images/0503/0859/6c7d6.png)
![\sqrt[5]{32}=\sqrt[5]{2^{5}}](/tpl/images/0503/0859/ad486.png)
![\sqrt[5]{2^{5}}=2^{\frac{5}{5}}=2](/tpl/images/0503/0859/67bfa.png)
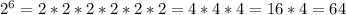
Объяснение:
.....................