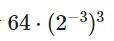
Объяснение:
1) 3х - 7 < x + 1,
3x - x < 1 + 7,
2x < 8,
x < 4.
ответ: х ∈ (-∞; 4).
2) 2 + x > 8 - x,
x + x > 8 - 2,
2x > 6,
x > 3.
ответ: х ∈ (3; +∞).
3) 1 - x ≥ 2x - 5,
-x - 2x ≥ -5 - 1,
-3x ≥ -6,
x ≤ 2.
ответ: х ∈ (-∞; 2].
4) 2x + 1 > x + 6,
2x - x > 6 - 1,
x > 5.
ответ: х ∈ (5; +∞).
5) 4x + 2 > 3x + 1,
4x - 3x > 1 - 2,
x > -1.
ответ: х ∈ (-1; +∞).
6) 6x + 1 < 2x + 9,
6x - 2x < 9 - 1,
4x < 8,
x < 2.
ответ: х ∈ (-∞; 2).
То есть получаем, что 2 в 6 Степни равна 64.
Если в примере дано число со степенью и за скобкой ещё степень. То внешнюю степень (она за скобкой) умножаем на внутреннюю ( степень внутри скобки).
То есть (2 в минус 3 степени) в 3 степени, мы не трогаем основу, то есть цифру 2, а просто умножаем степень на степень, то есть -3 * 3 = -9
И у нас выходит 2 в минус 9 Степени.
А теперь при умножений чисел со степенями, если есть возможность приравнять основу к одному числу, пользуемся этой возможностью.
Зная, что 64 это 2 в 6 степени и его умножили на 2 в минус 9 степени, переходим к правилу. Если у основания степеней одни и те же числа. То основание не трогаем, а работает со степенями. То есть если 2^1 * 2^5 то это равняется к 2 ^ (1+5) = 2^6 степени. Если дело обстоит с делением, то основание не трогаем, а занимаемся степенями. То есть если в случае 2^1 : 2^5 = 2^1-5= 2^-4
А теперь если степень отрицательное число, то число со степенью отпускается вниз, чтобы избавится от минуса. То есть 2^-4 мы должны писать как 1/2^4 или 1/16
В примере
64*(2^3)^-3
Приводим к общему основанию
2^6 * (2^3)^-3
Теперь умножаем степень на степень и избавляемся от скобки
2^6 * 2^-9
Так как основания одни, но степень разные. Прибавляем степени, так как у нас знак умножения
2^6+(-9) = 2^-3
Вспоминаем правило, при вычитании чисел, от большего отнимаем меньшее и ставим знак большего, то есть мы от 9 отняли 6, и поставили знак числа 9
Теперь, так как ответ 2^-3 в минусовой степени. Наше число переходит вниз
1/2^3 или 1/8