4.4 x₁= 0; x₂= -4
4.5 x₁= 1; x₂= -1
4.6 x₁= 2/3; x₂= -3; x₃= -3; x₄= -6
Объяснение:
4.4
│4x+8│+3=11
│4x+8│=8
4x+8=8; 4x+8= -8
4x=8-8; 4x= -8-8
4x=0; 4x= -16
x=0; x= -4
4.5
││x│+7│=8
│x│+7=8; │x│+7= -8
│x│=1; │x│= -15
x=1; x=-1 │x│= -15
x=1; x= -1
4.6
(x+3)*│x+1│= ((4-x)(x+3))/2
(x+3)*│x+1│= 1/2 (4-x)(x+3)
(x+1)(x+3) = 1/2 (4-x)(x+3); (x+1)(x+3) = - 1/2 (4-x)(x+3)
x²+4x+3 = 1/2 (x+3)(4-x); x²+4x+3 = -1/2 (x+3)(4-x)
x²+4x+3 = -x²/2 + x/2 +6; x²+4x+3 = x²/2 - x/2 -6
1/2 (3x-2)(x+3)=0; │*1/2 1/2 (x+3)(x+6)=0 │*1/2
(3x-2)(x+3)=0; (x+3)(x+6)=0
3x-2=0; x+3=0; x+3=0; x+6=0
3x=2; x= -3; x= -3; x= -6
x= 2/3; x= -3; x= -3; x= -6
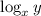Область Допустимых Значений (она же - ОДЗ) выглядит так (это нам понадобится для решения задачи):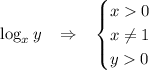 
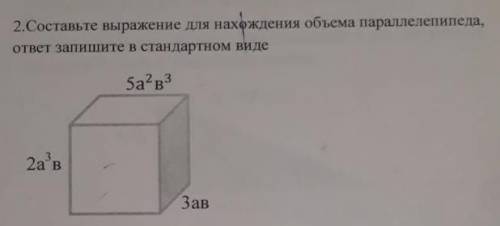
Рассмотрим логарифм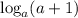 
. С точки зрения ОДЗ и того, что 
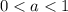и 
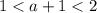, с этим логарифмом все хорошо.
Но, так как основание логарифма меньше единицы, то его значение больше ноля при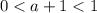 
, а меньше ноля - при 
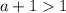. Из данного в задаче условия на 
имеем, что 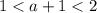. Значит, выражение этого логарифма отрицательно.
Но что тогда можно сказать о втором логарифме? Для него подлогарифмическое выражение меньше ноля, что нас абсолютно не устраивает.
Итог: выражение не имеет смысла.
B)Рассуждаем по аналогии:
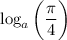- существует и больше ноля (так как 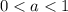и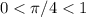 
). Основание и подлогарифмическое выражение не только соответствуют ОДЗ, но и оба меньше единицы.
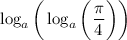- тоже существует, так как 
и 
, а также подлогарифмическое выражение больше ноля.
Итог: выражение 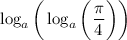имеет смысл.
Решаем с использованием уже оговоренных схем:
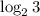- существует и больше единицы (так как 
).
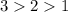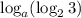- существует и меньше ноля (так как 
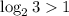и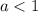 
).
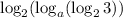- не очень хорошо существует, в силу отрицательности подлогарифмического выражения.
Итог: выражение не имеет смысла.
D)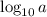
- существует и меньше ноля (так как 
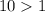и ).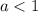
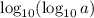- не существует, так как 
.
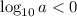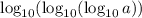- не существует, так как уже его подлогарифмическое выражение не существует.
Итог: выражение не имеет смысла.
ответ : B ) .
