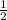a1=2
a2=1
прогрессия геометрическая, найдем знаменатель q:
q=a2/a1=1/2
тогда an=a1*q^(n-1)
Предположим, что 1/16 принадлежит, тогда найдем ее номер:
1/16 = 2*(1/2)^(n-1)
1/32 = (1/2)^(n-1)
(1/2)⁵ = (1/2)^(n-1)
n-1=5
n=6
Таким образом 6 член прогресии равен 1/16
Объяснение:
Обозначим за Х количество мест в ряду в 1-м зале
Тогда (Х+10) - количество мест в ряду во 2-м зале
420/Х - количество рядов в 1-м зале
480/(Х+10) - количество рядов во 2-м зале
420/Х-480/(Х+10)=5
приводим левую часть уравнения к общему знаменателю и складываем:
(420Х+4200-480Х)/Х(Х+10)=5
(4200-60Х)/(Х²+10Х)=5
делим обе части уравнения на 5:
(840-12Х)/(Х²+10Х)=1, или имеем право записать как:
840-12Х=Х²+10Х
Х²+22Х-840=0
Решая полученное квадратное уравнение, находим, что:
Х₁=20
Х₂=-42 данный корень не удовлетворяет условию задачи, поскольку количество мест в ряду не может быть отрицательным.
20 мест в ряду в 1-м зале
30 мест в ряду во 2-м зале (на 10 мест больше, чем в ряду первого зала)
21 ряд в 1-м зале
16 рядов во 2-м зале (на 5 рядов меньше, чем в первом зале
Да, является. Она будет 6
Т.к q=