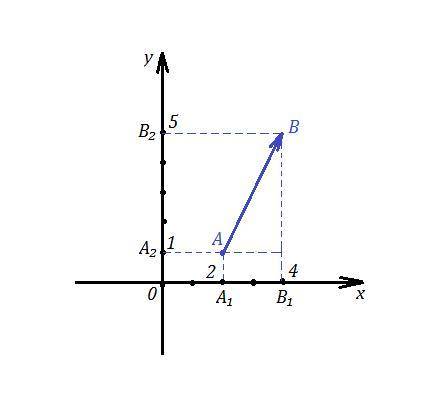
Необходимо начертить вектор АВ=(2;4) . Начало вектора выбрать произвольно.
Координаты вектора - это проекции вектора на оси ОХ и ОУ. То есть вектор АВ проектируется на ось ОХ в отрезок , длина которого равна 2 единицам, а на ось ОУ - в отрезок, длина которого 4 единицы. Причём, так как координаты положительные, то направление от проекции начала вектора к проекции конца вектора такое же, как и у осей координат.
Если , например, за начало вектора возьмём точку А(2,1), то от точки А₁(2,0) , которая является проекцией точки А на ось ОХ, отложим вдоль оси ОХ отрезок длиной 2 единицы в направлении оси ОХ, попадём в точку В₁(4,0), которая будет проекцией точки В на ось ОХ. А₁В₁ - проекция вектора АВ на ось ОХ.
Аналогично, от точки А₂(0,1) отложим вдоль оси ОУ отрезок длиной 4 единицы, попадём в точку В₂(0,5) . А₂В₂ - проекция вектора АВ на ось ОУ.
Затем соединим точку А(2,1) с точкой В(4,5), получим искомый вектор АВ=(2,4).
Sпо = 60 км - путь по течению.
Sпр = 32 км - путь против течения
T = 5 ч - полное время в пути
Vт = 2 км/ч - скорость течения
НАЙТИ
Vс = ? - собственная скорость
ВСПОМИНАЕМ
Скорости по течения - складываются, против течения - вычитаются.
Формула пути - S = V*t.
РЕШЕНИЕ
Запишем уравнение времени.
1)
Вспоминаем формулу -разность квадратов и приводим уравнение к общему знаменателю (и забываем о нём), подставляем известные значения. Неизвестную собственную скорость уже можно обозначить через - V.
2)
5*(V² - 4) = 60*(V-2) + 32*(V+2) = 92*V - 28*2
Упрощаем
3) 5*V² - 92*V - 36 = 0
Решаем квадратное уравнение и получаем
Дискриминант - D = 7744 и √7744 = 88
Получаем корни уравнения
V = 18 км/ч - собственная скорость - ОТВЕТ
ВНИМАНИЕ, ВНИМАНИЕ - второй корень уравнения - V = 0.4.
Не может быть - всего 0,4 км/ч и тоже будет 5 часов!
Проверяем.
60 км : 2,4 км/ч = 25 часов
- 32 км : 1,6 км/ч = - 20 часов.
Действительно: разность времени 5 часов. но время назад не вернёшь.
.