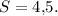
Объяснение:
Обозначим 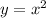 за
за 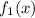 , а
, а 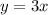 за
за 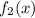 . Найдём сначала точки пересечения этих кривых:
. Найдём сначала точки пересечения этих кривых:
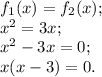
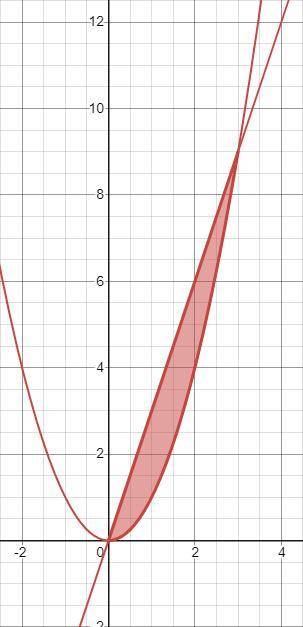
Получается, что это точки 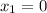 и
и 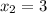 .
.
По рисунку видно, что 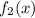 на отрезке
на отрезке ![x \in [0;\ 3]](/tpl/images/2007/6238/baef2.png) всегда больше, чем
всегда больше, чем 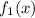 . Отметим также, что эти функции на этом интервале больше или равны нулю, то есть для нахождения площади фигуры не требуется разбивать область интегрирования на несколько отрезков. Отсюда следует, что площадь заключённой между этими кривыми фигуры будет равна разнице площадей фигур под графиками
. Отметим также, что эти функции на этом интервале больше или равны нулю, то есть для нахождения площади фигуры не требуется разбивать область интегрирования на несколько отрезков. Отсюда следует, что площадь заключённой между этими кривыми фигуры будет равна разнице площадей фигур под графиками 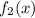 и
и 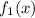 на отрезке
на отрезке ![[0;\ 3]](/tpl/images/2007/6238/72582.png) , то есть разнице интегралов от
, то есть разнице интегралов от 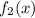 и
и 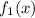 на отрезке
на отрезке ![[0;\ 3]](/tpl/images/2007/6238/72582.png) .
.
Найдём сначала первый интеграл:
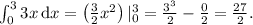
Теперь второй:
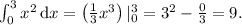
Найдём далее их разность, вычтем второй интеграл из первого:
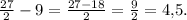
Это и есть площадь фигуры, ограниченной линиями 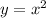 и
и 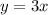 .
.
Дано:
sin α = ⅔
90° < α < 180°
Найти:
cos α
tg α
ctg α
• Выразим косинус через синус с основного тригонометрического тождества:
sin² α + cos² α = 1
cos² α = 1 - sin² α
cos α = √(1 - sin² α)
• Так как 90° < α < 180°, то α ∈ II четверти, ⇒ cos α < 0
cos α = - √(1 - sin² α) = - √(1 - (⅔)²) = - √(1 - 4/9) = - √(5/9) = -√5/3
• Находим тангенс через формулу:
tg α = sin α/cos α
tg α = ⅔ : (-√5/3) = - (⅔ • 3/√5) = -2/√5 = -2√5/5
• Находим котангенс через формулу:
ctg α = 1/tg α
ctg α = 1 : (-2√5/5) = -5/2√5 = -5√5/2 • 5 = -√5/2
cos α = -√5/3
tg α = -2√5/5
ctg α = -√5/2