С решениям!! Тест по теме: «Функция у = √х и ее график»
1.Какова область определения функции у = √х ?
а) х ≥ 0
б) у ≥ 0
в) х ≤0
2. Какова область значений функции у = √х ?
а) х ≥ 0
б) у ≥ 0
в) х ≤0
3.В какой координатной четверти находиться график функции
у = √х ?
а)1
б)2
в)3 и 4
4. Функция задана формулой у = √х , чему равно значение функции , если значение аргумента равно 4 ?
а)16
б) 2
в)8
5. Функция задана формулой у = √х , чему равно значение аргумента, если значение функции равно 9?
а)3
б)81
в)9
6.Между какими двумя последовательными целыми числами находиться на координатной прямой число: √11
а)10 и 12
б)3 и 4
в)9 и 12
7.Укажите все целые числа, расположенные на координатной прямой между числами √7 и √24
а)8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23
б)2,3,4
в)2,3,4,5
8.При каких целых значениях x выполняется неравенство:
6 ≤ √х ≤ 16
а) х=7,8,9,10,11,12,13,14,15
б) х= √7, х= √8, х=3, х= √8, х= √(10 ), х= √(11,)…. х= √15
в) х=3
9.Через какую из данных точек проходит график функции у = √х
а)А(16;4)
б)В(4;16)
в)С(-16;4)
10.Не выполняя построения, найдите координаты точки пересечения графика функции у = √х и у = 9
а)(9;3)
б)(81;9)
в)(9;81
11.Построить и прочитать график функции y = -
12. Построить график функции: а) y=√х+2, y=√(x-1)
13.Найти наименьшее и наибольшее значения функции у = на отрезке: [0, 4]; б) [1, 5].
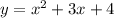


 :
:
 :
: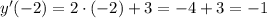
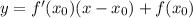


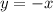
 касательной
касательной 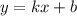 численно равен тангенсу угла наклона
численно равен тангенсу угла наклона 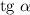 с положительным направлением оси
с положительным направлением оси 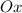
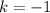 , следовательно,
, следовательно, 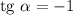 при
при  или
или 
 или
или 
Панель управления (англ. Control Panel) является частью пользовательского интерфейса Microsoft Windows. Она позволяет выполнять основные действия по настройке системы, такие, как добавление и настройка устройств, установка и деинсталляция программ, управление учётными записями, включение специальных возможностей, а также многие другие действия, связанные с управлением системой. Апплеты (значки) Панели управления, с которых можно выполнять определенные системные действия, представляют собой файлы с расширением .cpl. Большинство таких файлов расположено в системных папках C:\Windows\System32 и C:\Windows\winsxs (в папках внутри этой папки). Каждый такой апплет запускает системную утилиту, которая выполняет соответствующее действие, связанное с настройкой либо управлением операционной системой. Большинство апплетов в Панели управления соотносятся с определенными системными утилитами производства Microsoft, но в некоторых случаях сторонние производители также добавляют свои значки в Панель управления Windows 7 для достижения большего удобства управления своим программным либо аппаратным продуктом. Впервые Панель управления появилась в Windows 2.0. Многие из ныне существующих апплетов были добавлены с новыми релизами операционной системы. Со временем апплетов стало достаточно много, и это послужило поводом для сортировки их по категориям. Теперь пользователь волен самостоятельно выбирать наиболее удобный для него режим просмотра.
Объяснение: