121. Вычислите сумму и разность и проверьте результат прикидкой а) 534 4 129
б) 5 319 4 8 642
в) 18 644 +7 974
r) 421 - 198,
д) 65 432 - 12 345;
е) 56 546 - 8 748
Рауалнам
8
122. в бочке 100 литров масла (рис. 8). Как можно
отлить из бочки а) 10 литров; б) 50 литров мас-
ла, если имеются емкости объемами 30 и 70
100 л
Петров?
70 л
) (
Волим дома
123. Вычислите сумму и разность и проверьте результат прикидкой
а) 253 6127 в) 7 300 + 16 344
д) 889 610 + 18 006
б) 4210 - 1987 г) 905 765 - 120 666 е) 231 887 - 98 987
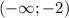
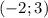(рис. 2)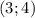
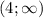
1) а) (a - 4)(a - 2) = a^2 - 6a + 8
б) (3x + 1)(5x - 6) = 15x^2 - 13x - 6
в) (3y - 2c)(y + 6c) = 3y^2 + 16cy - 12c^2
г) (b + 3)(b^2 + 2b - 2) = b^3 + 5b^2 + 4b - 6
2) а) 2x(a - b) + a(a - b) = (a - b)(2x + a)
б) 3x + 3y + bx + by = 3(x + y) + b(x + y) = (x + y)(3 + b)
3) 0,2y(5y^2 - 1)(2y^2 + 1) = (y^3 - 0,2y)(2y^2 + 1) =
= 2y^5 - 0,4y^3 + y^3 - 0,2y = 2y^5 + 0,6y^3 - 0,2y
4) а) 3x - xy - 3y + y^2 = x(3 - y) - y(3 - y) = (3 - y)(x - y)
б) ax - ay + cy - cx - x + y = a(x - y) - c(x - y) - (x - y) = (x - y)(a - c - 1)
5) Размеры клумбы: x и x+5 м.
Площадь дорожки 26 кв.м., а ширина 1 м. Дорожка показана на рис.
2x + 2(x+5) + 4 = 26
x + x + 5 + 2 = 13
2x = 13 - 7 = 6
x = 3 м - ширина клумбы.
x + 5 = 3 = 5 = 8 м - длина клумбы.