1 - 150 (1)
2 - 210 (2)
3 - 168 (3)
Объяснение:
Решение через проценты:
Представим что первая типография выпустила 100% книг, значит вторая выпустит на 40% больше, т.е. 140%Если 140% выпустила вторая типография, то третья типография выпустит 140% · 4/5 = 112% Суммируем проценты и находим один процент от общего кол-ва книг: 100 + 140 + 112 = 352; 528:352 = 1.5 Первая типография: 100 · 1.5 = 150 (1); Вторая типография: 140 · 1.5 = 210 (2); Третья типография: 112 · 1.5 = 168 (3);Что-бы убедиться в правильности решения, можем найти их сумму:
150+210+168 = 528
Решение через части:
Первая типография:
Вторая типография: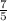 
Третья типография: · 
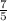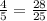Сумма: 
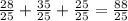Найдем 1/25 часть 
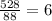Первая типография: 25 * 6 = 150 (1); Вторая типография: 25 * 35 = 210 (2); Третья типография: 25 * 28 = 168 (3);
Дано: прямоугольный Δ
a; b - катеты
S=90 см²
S₁+S₂ = а²+b² =369 см₂
a-? b-?
Решение
1) Первое уравнение получаем из условия:
а²+b² = 369
2) Площадь прямоугольного треугольника равна половине произведения катетов, получаем второе уравнение:
3) Решаем систему: (a>0; b>0)
a≠0
Замена: а²=t ( t > 0)
Решаем уравнение:
t² - 369t + 32400 = 0
D = 369² - 4·1·32400 = 136161 - 129600 = 6561 = 81²
t₁ = (369-81)/2 = 144
t₂ = (369+81)/2 = 225
Обратная замена:
При t₁ = 144 => a² = 144 => a₁ = - √144 = - 12 < 0
a₂ = √144 = 12 > 0
При t₂ = 225 => a² = 225 => a₃ = - √225 = - 15 < 0
a₄ = √225 = 15 > 0
Зная а₁=12 и а₂ = 15, найдем b
b₁ = 180/12 = 15
b₂ = 180/15 = 12
Получаем два решения взаимозаменяемых:
а=12; b=15
а=15; b=12
ответ: 12 см; 15 см - катеты