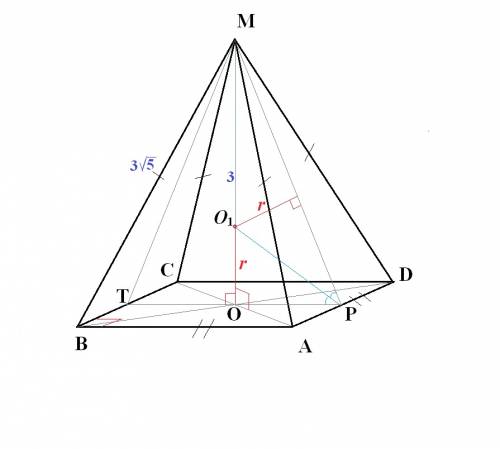
Чертеж во вложении.
Пирамида МАБСД. МО=3 -высота, МВ=МА=МС=МД=3√5.
О₁ - центр вписанной сферы.
АВСД - квадрат, О-центр вписанной и описанной окружностей.
∆ВМО-прямоугольный. По теореме Пифагора
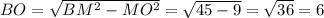
∆ВОA-прямоугольный, ОВ=ОА. По теореме Пифагора
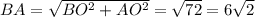
Тогда ОР=1/2АВ=3√2.
В прямоугольном ∆МОР по теореме Пифагора
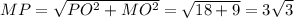
О₁ - центр вписанной сферы, является центром вписанной в ∆ТМР окружности. Для этой окружности и для сферы r=ОО₁.
Тогда О₁ - точка пересечения биссектрис ∆ТМР.
Рассмотрим прямоугольный ∆МОР. РО₁-биссектриса. МО₁=МО-ОО₁=3-r.
По свойству биссектрисы треугольника
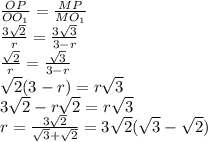
Площадь сферы:
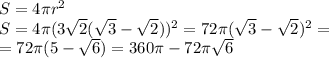
3y=12
х+у+z=7
x-2y+2z=-3
1)y=4
2)х+4+z=7 Подставляем y в 3) и 2)
3)x-2*4+2z=-3
y=4
х=3-z Выражаем x
(3-z)-8+2z=-3 Подсавляем вместо х значение 3-z
y=4
х=3-z
z-5=-3 Раскрываем скобки
y=4
х=3-z Подставляем z
z=2
y=4
х=1
z=2
х=2у
3x-2y-z=1
5x+4y-2z=8
x=2y
4y-z=1
14y-2z=8
x=2y
z=4y-1
14y-2*(4y-1)=8
x=2y
z=4y-1
y=1
x=2
y=1
z=3
сделай лучшим
для меня это важно