Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
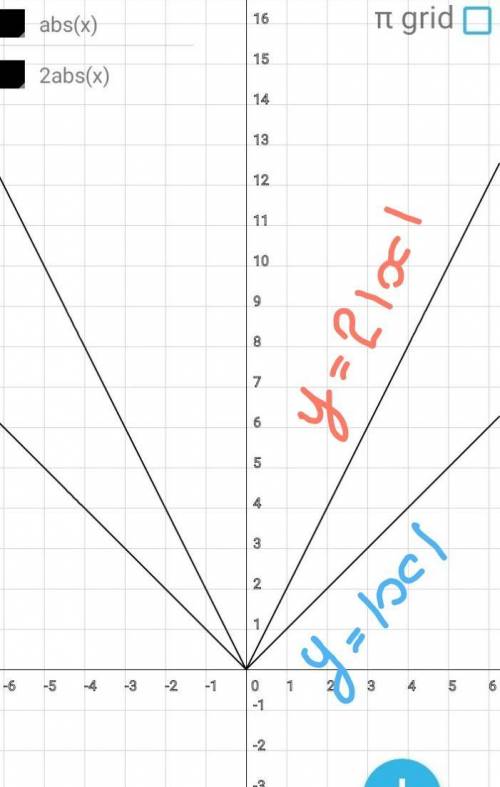
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
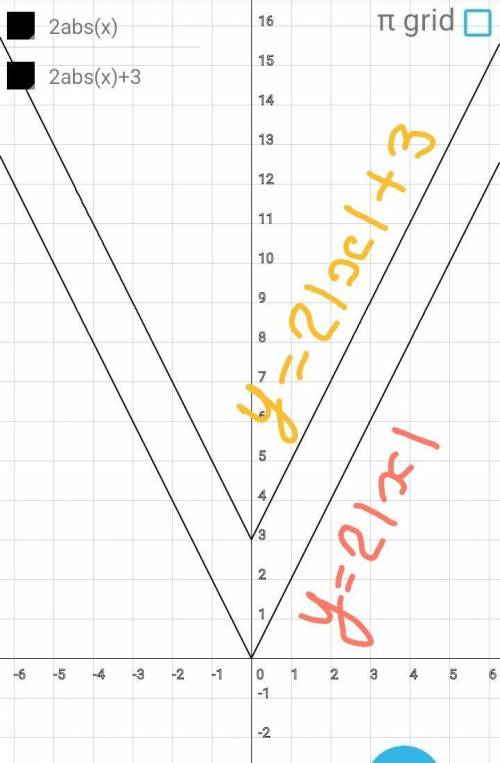
Шаг 3.
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
Посмотрите на фото
Объяснение: