1 действие: Кладём гирю (8кг) и мешок (50кг) на 1-ую чашу весов и из мешка (50кг) уравновешиваем весы. Получаем на весах гирю (8кг) + мешок (21кг) = мешок (29кг).
2 действие: Кладём мешок (29кг) на 1-ую чашу весов и гирю (8кг) на 2-ую чашу весов, после этого из мешка (29кг) отвешиваем мешок (8кг). Получаем в стороне мешок (21кг) и на весах мешок (8кг) = гирю (8кг).
3 действие: Кладём мешок (8кг) на 1-ую чашу весов и уравновешиваем весы. Получаем мешок (4кг) = мешок (4кг).
4 действие: Кладём мешок (4кг) на 1-ую чашу весов и уравновешиваем весы. Получаем мешок (2кг) = мешок (2кг).
5 действие: Кладём мешок (2кг) на 1-ую чашу весов и уравновешиваем. Получаем мешок (1кг) = мешок (1кг).
Кладём в ответ мешок (21кг) и мешок (1кг)
Объяснение
Коэффициент при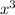 равен
равен 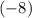 .
.