
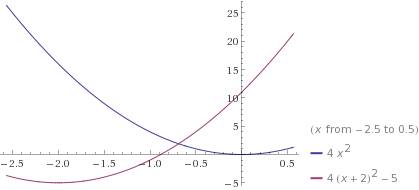
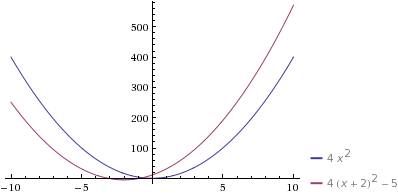
если для первого графика y = 4x^2 вершина находится в точке (0;0), то
ось симметрии параболы - ось OY (уравнение x=0)
то для второго графика ось симметрии сместится влево на 2 (уравнение x = -2, все первое слагаемое обратится в 0 и получится y = -5), т.е. для второго графика вершина опустится вниз по оси OY на 5 единиц и сместится влево на 2 единицы по оси OX
координаты вершины новой параболы (-2;-5), ветви вверх и она в точности повторяет первый график (из новой точки---новой вершины), иными словами
новый график получится параллельным переносом исходного графика вниз по оси OY на 5 единиц и влево по оси OX на 2 единицы
Даны координаты вершины треугольника ABC :А(1;0) ,В(13;-19),С(17;13) найти уравнение стороны АВ и АС и их угловые коэффициенты.
Находим векторы.
АВ = В(13;-19) - А(1;0) = (12; -19). По координатам вектора сразу определяется угловой коэффициент прямой АВ.
к(АВ) = Δу/Δх = -19/12.
Уравнение АВ: (x- 1)/12 = y/(-19) каноническое, или
19x + 12y - 19 = 0 общего вида, или
у = (-19/12)х + (19/12) с угловым коэффициентом.
АС = С(17;13) - А(1;0) = (16; 13). По координатам вектора сразу определяется угловой коэффициент прямой АС.
к(АС) = Δу/Δх = 13/16.
Уравнение АС: (x- 1)/16 = y/13) каноническое, или
13x - 16y - 13 = 0 общего вида, или
у = (13/16)х - (13/16) с угловым коэффициентом.