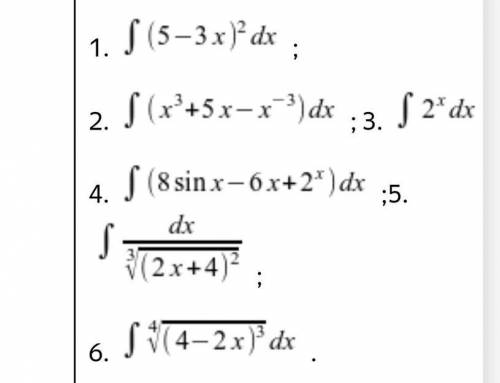
Пусть x ч-время работы первой трубы, y ч-время работы второй трубы. Тогда 1/x - производительность первой трубы, 1/y - производительность второй трубы. Составим первое уравнение системы: 1/x+1/y=1/14.
1,5/x - новая производительность первой трубы. Составим второе уравнение системы:
1,5X+1/y=1/12/
Составим систему уравнений:
1/x+1/y=1/14
1,5/x+1/y=1/12
Решим алгебраического сложения. Вычтем из первого уравнения второе. Получим:
-0,5/x+0=1/14-1/12
-0,5/x=6/84-7/84
-0,5x=-1/84
x=0,5*84
x=42
Значит, время работы первой трубы - 42 часа. Тогда подставим вместо х 42 в первое уравнение системы, получим: 1/42+1/y=1/14, 1/y=1/14-1/42, 1/y=3/42-1/42, 1/y=2/42, 1/y=1/21, y=21. Значит, работая отдельно, вторая труба наполнит бассейн за 21 час.
ответ: 21 час.
Объяснение: (И - обозначение интеграла, ^ -знак степени)
1) =И (25-30x+9x^2) dx=25x-30x^2 /2 +9x^3 /3+c=25x-15x^2+3x^3+c
2) =x^4/ 4 +5x^2 /2-x^-2/ -2 +c=x^4/ 4+2,5x^2 +x^-2/ 2+c
3) =2^x/ ln2 +c
4) =-8cosx-6x^2/ 2 +2^x/ ln2+c=-8cosx-3x^2+2^x/ ln2+c