Пусть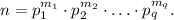 
Обращаю Ваше внимание, что я не собираюсь использовать четность числа различных простых делителей числа p. Обращаю также Ваше внимание, что в условии не сказано, в каком порядке берутся простые делители числа p. Также я не буду использовать равенство числа положительных и числа отрицательных слагаемых. Итак, можно считать, что нам дана сумма
сократив на общие множители, получаем
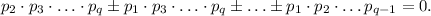
Поэтому 
Поскольку правая часть делится на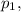 
левая часть также обязана делиться на 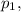а это очевидно не так.
Вывод: такое равенство не может иметь место.
1 / cos(x)^2 - 3 / cos(x) + 2 = 0
так как cos(x) != 0, так как иначе было бы деление на 0, а этого делать нельзя, то умножим обе части уравнения на cos(x)^2. Получаем:
1 - 3cos(x) + 2cos(x)^2 = 0
переставим слагаемые в удобном для нас виде:
2cos(x)^2 - 3cos(x) + 1 = 0
Заметим, что это квадратное уравнение относительно cos(x). Решим его:
D = (-3)^2 - 4 * 2 * 1 = 9 - 8 = 1
cos_1(x) = (-(-3) + sqrt(1)) / (2 * 2) = (3 + 1) / 4 = 4 / 4 = 1
cos_2(x) = (-(-3) - sqrt(1)) / (2 * 2) = (3 - 1) / 4 = 2 / 4 = 1 / 2
cos(x) = 1 при x = 2пn, где n - целое
cos(x) = 1 / 2 при x = п / 4 + 2пk, где k - целое
Наш ответ это совокупность решений для этих двух корней.
ответ: x = 2пn, где n - целое U x = п / 4 + 2пk, где k - целое