Условие. Y²+xy-4x-9y+20=0 ; y=ax+1 ; x>2
найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).
Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим
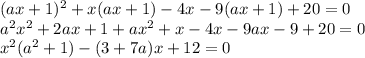
Найдем дискриминант квадратного уравнения относительно x
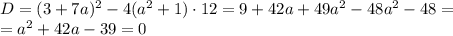
Получим 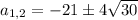
Если подставить 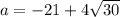 , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение  , у которого корень
, у которого корень
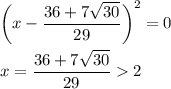
Если подставить  , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение 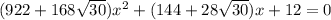 , у которого корень
, у которого корень
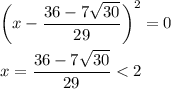
ответ: 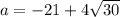
1) Если x₀=y₀, то |x₀|=1/2=|y₀|, откуда а=1/2. Из неравенства
|x+y|≤|x|+|y|≤√(2(x²+y²)) верного для всех х,у при а=1/2 получаем
2-|x|-|у|≤|x|+|y|≤1, т.е. |x|+|y|=1. Подставляя это во второе уравнение системы, получим 4 точки, из которых подходят только две: (1/2;1/2) и (-1/2;-1/2). Т.е. при а=1/2 система действительно имеет только 2 решения.
2) Если x₀=-y₀, то |x₀|=1=|y₀|, откуда а=2. Из неравенства
2|x|=|(x+y)+х+(-у)|≤|x+у|+|x|+|y|=2, следует что |x|≤1 и аналогично |y|≤1, а значит x²+y²=2 может быть только если |x|=1 и |y|=1. Из 4 точек подходят только две (-1;1) и (1;-1), значит при а=2 система тоже имеет только 2 решения. Итак, ответ: а∈{1/2; 2}.