«Просчитав» несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды. Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k + 1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
«Просчитав» несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды. Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k + 1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Объяснение:
Пусть х - натуральная степень числа 4. ⇒
Докажем, что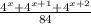 - целое число.
- целое число.
4ˣ⁻¹ - целое число.