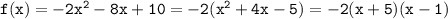; (график во вложении, если не понял)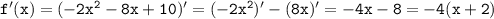
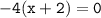, следовательно, производная имеет единственную критическую точку 
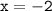; интервалы нам дают следующее: производная отрицательна на промежутке 
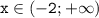, следовательно, функция на этом промежутке убивает, и наоборот, – возрастает функция на промежутке 
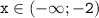, потому что производная на данном промежутке положительна.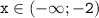 
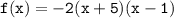должна быть положительна, следовательно, неравенство мы получаем следующее: 
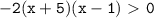; решение неравенства: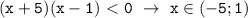 
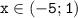
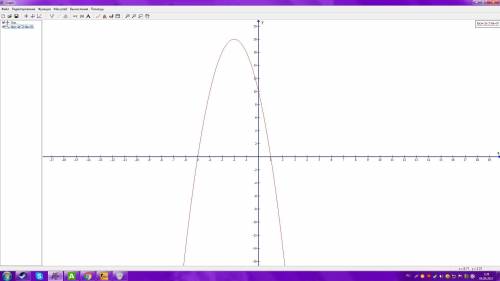
Учтём, что 0,2 = 1/5 = 5⁻¹
Теперь наш пример:
(х - 9)/(5 - 5ˣ⁻¹⁰) ≥ 0
Метод интервалов. ищем нули числителя и знаменателя:
а) х - 9 = 0
х = 9
б) 5 - 5ˣ⁻¹⁰ = 0
5ˣ⁻¹⁰ = 5
х - 10 = 1
х = 11
теперь числовая прямая:
-∞ [9] (11) +∞
- + + знаки (х - 9)
+ + - знаки (5 - 5ˣ⁻¹⁰ )
решение неравенства
х∈ [9; 11)
целые решения: 9 и 10
ответ: 90