В решении.
Объяснение:
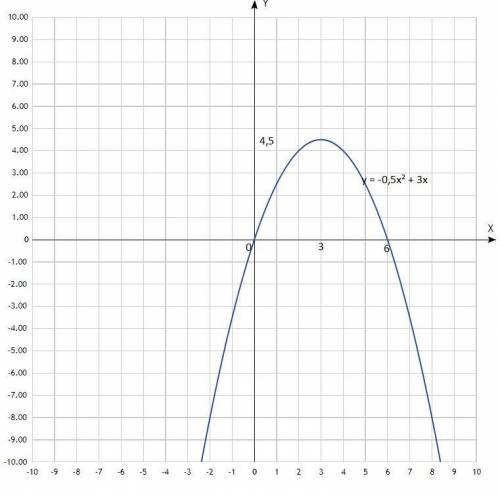
Дана функция у = -1/2 х² + 3х; найти промежуток её убывания.
Построить график функции.
Сначала преобразовать уравнение функции для упрощения.
-1/2 х² + 3х = -0,5х² + 3х, неполное квадратное уравнение.
Приравнять к нулю:
-0,5х² + 3х = 0
0,5х (-х + 6) = 0
0,5х = 0;
х₁ = 0;
-х + 6 = 0
-х = -6
х = 6;
График - парабола, ветви направлены вниз, пересекают ось Ох в точках: х = 0; х = 6 (нули функции).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2 4 6 8
у -8 -3,5 0 2,5 4 4 0 -8
По вычисленным точкам построить параболу.
Согласно графика, функция убывает в промежутке х∈(3; +∞).
ответ: 50 м и 60 м
Объяснение: Пусть длина участка x м, а ширина - y м, тогда площадь участка равна xy, а периметр равен 2·(x + y).
Составим систему уравнений:
xy = 3000
2x + 2y = 220
Второе уравнение разделим на 2:
xy = 3000
x + y = 110
Решим систему подстановки:
xy = 3000
x = 110 - y
(110 - y)·y = 3000
110y - y² = 3000
-y² + 110y - 3000 = 0
y² - 110y + 3000 =0
D = b² - 4ac = (-110)² - 4·3000 = 12100 - 12000 = 100
x₁ = 110 + √100 / 2 = 110 +10 / 2 = 60
x₂ = 110 - 10 / 2 = 50
y₁ = 110 - 60 = 50
y₂ = 110 - 50 = 60
Решением системы являются две пары чисел (60; 50) и (50; 60). Следовательно, стороны прямоугольника равны 50м и 60м.