
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
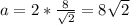 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
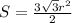 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

1) (x+m)(y+m)=xy+xm+my+m²
2) (x+8)(x-1)=x²-x+8x-8=x²+7x-8
3) (-a+y)(-y-2)=ay+2a-y²-2y
4) (a-4)(2a+1)=2a²+a-8a-4=2a²-7a-4
5) (2x-1)(2x+y)=4x²+2xy-2x-y
6) (m-n)(x+y)=mx+my-nx-ny
7) (5-a)(4-a)=20-5a-4a+a²=a²-9a+20
8) (6m-3)(2-5m)=12m-30m²-6+15m=-30m²+27m-6