sinx·cosx = -√3/4 потому что cos(-x) = cosx
1/2·sin2x = -√3/4 формула синуса двойного угла: sin2x = 2sinx·cosx
sin2x = -√3/2 умножили на 2 обе части
2x = (-1)^(n+1)·π/3 + πn , n∈Z
x = (-1)^(n+1)·π/6 + πn/2 , n∈Z - ответ
(-1)^(n+1) - это "минус единица в степени (n + 1)@
2sin(x/2)cos(x/2)+cos²(x/2)-sin²(x/2)-sin²(x/2)-cos²(x/2)=0
2sin(x/2)cos(x/2)-2sin²(x/2)=0
2sin(x/2)*(cos(x/2)-sin(x/2))=0
sin(x/2)=0⇒x/2=πn⇒x=2πn,n∈z
cos(x/2)-sin(x/2)=0/cos(x/2)
1-tg(x/2)=0
tg(x/2)=1⇒x/2=π/4+πk⇒x=π/2+2πk,k∈z
Объяснение:
см, тогда второй катет - 
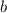см. Площадь прямоугольного треугольника равна 
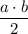, что составляет 210 см² или перепишем сразу 
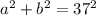
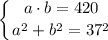
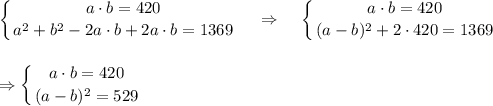
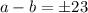. Тогда имеем несколько случаев.
, то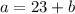 
и подставим в первое уравнение.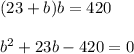
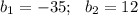см и корень 
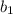не удовлетворяет заданному условию
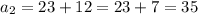см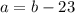
,то подставив в первое уравнение, получим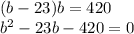
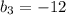
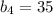см и корень 
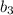не удовлетворяет условию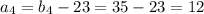
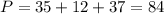см
а) x²+x-x/x+1 = x²/x+1
б) (m+2)(m+4)-4m/4m(m+4) = m²+4m+2m+8-4m/4m(m+4) = m²+2m+8/4m(m+4)
в) x²-xy+xy+y²/(x+y)(x-y) = x²+y²/(x+y)(x-y)
г) 3xy²+3x²y+y³+xy²-x³-x²y-3x²y-3xy² / (x²+xy)(y²+xy)=y³+xy²-x³-x²ý / (x²+xy)(y²+xy)