1. Среди действительных чисел 0,9; √(2 ) ; 3/5 ;6,(3); √25 выберите иррациональное число. А) 6,(3)
В) 0,9
С) √25
D) 3/5
E) √2
[1]
2. К какому из интервалов действительных чисел принадлежит число √7.
А) (2,1; 2,7)
В) (-0,1; 2,6)
С) (2; 2,5)
D) (0; 2,6)
E) (1,1; 1,8)
[1]
3. Вычислите рациональным
[2]
4. Расположите в порядке убывания: 5√3, √87, 4√5
[2]
5. Освободитесь от иррациональности в знаменателе дроби: 28/√7
[3]
6. Высота моста над рекой выражена числом √28 м. Сможет ли пройти под этим мостом судно, высота которого над уровнем воды 5,6 м?
[2]
7. Упростите выражение: (b/(√ab-a)-√a/(√b-√a))∙((√a-√b)a)/(a-b), а>b, b>0, a≠b
[4]
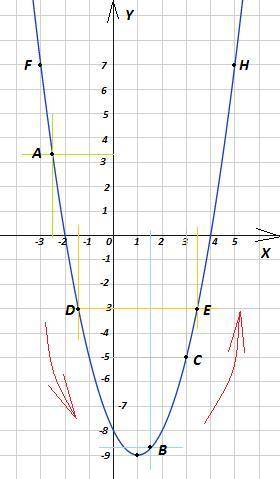
8. Дана функция у=√х:
а) График которого проходит через точку с координатами А(а;8√2). Найдите значение а.
b) Если х ϵ [0; 16], то какие значения будет принимать данная функция?
с) y ϵ [11; 24]. Найдите значение аргумента.
d) Найдите при каких х выполняется неравенство у ≤ 4.
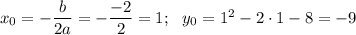
Отметь как лучший,буду рад!
1)Множество целых чисел Z включает в себя число 0, множество натуральных чисел и отрицательные числа .
2) Множество рациональных чисел Q включает в себя множество целых чисел Z и все дробные числа.
3) Вместо фразы m – целое число можно писать Z .
4) Вместо фразы r– рациональное число можно писать Q.
5) N – множество натуральных чисел множества Z , Z – множество целых чисел множества Q.
6) Повторяющая группа цифр после запятой в записи десятичной дроби называется периодом, а сама дробь называется периодической.
7) Множество Q рациональных чисел - это множество чисел вида m/n ,
где - m целое число, n – натуральное число , или как множество обыкновенных дробей.
Объяснение: