(2x-3)^2>1
4x^2-12x+9>1
4x^2-12x+8>0
D=144-4*4*8=16
корень из D=4
x1,2=12+-4/8
x1=2
x2=1
следовательно, 1<x<2
вроде бы,так
затем,надо построить прямую, отметить на ней точки 1 и 2,построить параболу,отметить где плюс и минус и выбрать промежутки,подходящие к условию неравенства.
всвязи с этим, получаем промежуток [1;2]
ответ: [1;2]
Объяснение: 
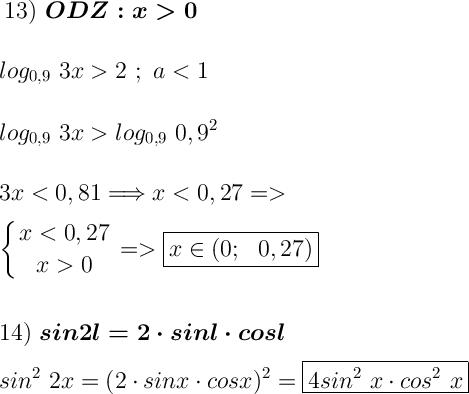
Доказательство:
Дана последовательность
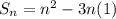
Допустим, что эта последовательность арифметическая прогрессия, тогда
при n = 1 получаем
при n = 2
и
а₂ = -2 - а₁ = -2 + 2 = 0
Таким образом разность арифметической прогрессии
d = a₂ - a₁ = 0 + 2 = 2
По известной формуле найдем n-й член арифметической прогрессии
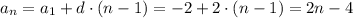
Известно, что сумма n членов арифметической прогрессии
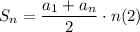
Докажем, что выражение (2) тождественно выражению (1) при
a₁ = -2 и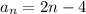 
, подставив в (2)
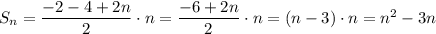
Тождество доказано.
Следовательно, последовательность, определённая суммой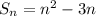 
является арифметической прогрессией.
4х^2-12x+8>0
через дискриминант
дискриминант=144-128=16
Х1=2
Х2=1