На перевёрнутом листе бумаги написано целое число. Учитель про него сообщил несколько фактов, затем признался, что дважды говорил правду и дважды солгал. Ученикам требуется узнать число, записанное на листе
бумаги.
Факт 1. Удвоенное число больше 95.
Факт 2. Это число меньше 61.
Факт 3. Учетверённое число больше 45.
Факт 4. Это число больше 7.
Какое число записал учитель?
(Если ответов несколько, запиши всё через запятую в порядке возрастания без пробелов.)
ответ:
ответить!
Koi
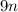
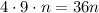
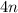
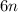

![[4,6]=2\cdot 2\cdot 3=12](/tpl/images/0629/9227/9a182.png)
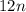
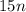
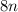
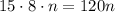
9y² + 12xy практически создают квадрат суммы, дополним это выражение:
9y² + 12xy + 4x² = (3y + 2x)², заметим, что это выражение есть целое число в квадрате.
5x² + 12xy + 9y² + 6x + 34 = x² + (4x² + 12xy + 9y²) + 6x + 34 = (3y + 2x)² + x² + 6x + 34
x² + 6x также дополняем до полного квадрата:
x² + 6x + 9 = (x + 3)²
(3y + 2x)² + x² + 6x + 34 = (3y + 2x)² + x² + 6x + 9 + 25 = (3y + 2x)² + (x + 3)² + 25
25 = 5² (целое число в квадрате)
(3y + 2x)² + (x + 3)² + 25 = (3y + 2x)² + (x + 3)² + 5²
Итак, получившееся выражение однозначно при любых целых x и y можно представить в виде суммы квадратов трёх натуральных чисел.