Теперь перейдем к вопросу о том, что делать, если у дробей будут разные знаменатели. Например, как нам сложить и
... А. А. Ахматова начала писать свою поэму «Реквием» в 1935 году, когда ее единственный сын Лев Гумилев был арестован. Вскоре его ...
Комплексный анализ поэмы Ахматовой «Реквием -
Поэма «Реквием» (вместе с «Поэмой без героя») стала итогом творческого пути ... Ахматова обращается к «памяти жанра» — в предисловии звучит цитата из ... В следующих частях поэмы развивается образ лирической героини ... Как развивается трагическая тема в поэме А. А. Ахматовой «Реквием»?
17
Объяснение:
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
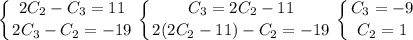
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит,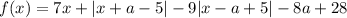 
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
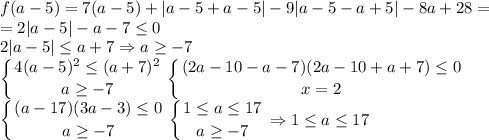
Наибольшее значение параметра — 17.
Присмотревшись к системе внимательно, замечаем, что это - система линейных уравнений, поскольку переменные x и y входят в неё в первых степенях.
Следовательно, решаем её как и любую линейную систему: подстановкой.
Из первого уравнения выражаем y и подставляем во второе:
Подставляем во второе:
Здесь я выделил коэффициент при x, зависящий от параметра, а, кроме того, кубический многочлен от параметра разложил на множители для большего удобства.
Теперь рассматриваем уравнение как линейное(с переменной x).
Очевидно, для любого линейного уравнения возможны следующие три случая:
а)Уравнение имеет ровно одно решение;
б)Уравнение имеет бесконечное множество решений;
в)Уравнение вообще не имеет решений.
Для начала стоит рассмотреть частные случаи.
а)Пусть . Тогда после подстановки получаем уравнение
, которое представляет из себя верное равенство(при умножении на 0 всегда получаем 0), а потому верно для любого x.
б)Пусть . Аналогичная ситуация имеет место. Уравнение вновь имеет бесконечно много решений, следовательно, и вся система(поскольку каждому x соответствует ровно один y, то бесконечному количеству значений x соответствует бесконечное количество значений y).
в)Пусть теперь .
Тогда сокращаем обе части уравнения на общий множитель:
То есть, для всех таких значений параметра а всегда имеет ровно 1 решение линейного уравнения(равное a-1). Тогда сразу из другого уравнения находим y:
таким образом, ответ можно записать так:
ответ: если , система имеет бесконечно много решений;
если , то система имеет единственное решение
Объяснение: