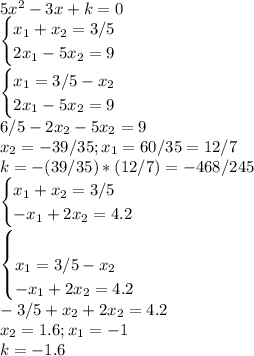Найдите свободный член квадратного уравнения 5х^2 -3х +k =0, корни которого х1 и х2, если: а) 2*х1 - 5*х2 =9 б) -х1 + 2*х2 =4.2 если можно, то с подробным решением, а то тему пропустила((
Общий ход построения данных графиков: График - прямая, для построения требуется две точки. Чертим координатную плоскость, подписываем оси и отмечаем положительное направление стрелками: вправо по оси х и вверх по оси у. Отмечаем центр – точку О и единичные отрезки по обеим осям в 1 клетку. Далее заполняем таблицу (для каждого графика свою, приведена ниже): Х= У= Отмечаем точки в системе координат, проводим через них прямую. Подписываем график. Всё! Итак, начнём:
у=-4х - прямая, проходящая через начало координат , поэтому достаточно ещё одной точки, например х=1, у= -4 , ставим точку (1;-4) и проводим прямую через эту точку и начало координат.
http://edu.glavsprav.ru/info/teorema-vieta/