ответ:Всего
Объяснение:Обратим внимание на то, что требуется сделать букет из 7 цветов так, чтобы в нем было хотя бы три красных тюльпана, а на количество белых тюльпанов ограничений нет. Тогда, заключаем, что в букете
1) в точности 7 тюльпанов;
2) наименьшее количество красных тюльпанов 3;
3) наибольшее количество красных тюльпанов 7.
По условию количество красных тюльпанов в саду 10, то все эти 3 пункта возможны. Обозначим белые тюльпаны через 0, а красные тюльпаны через 1. Так как порядок размещения не даёт новые то получаем следующие
0000111
0001111
0011111
0111111
1111111
Всего
(см. объяснение)
Объяснение:
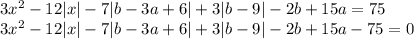
Введем функцию  .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке 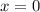 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров  и
и 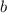 .
.
Уравнение  может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 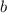 только, если
только, если 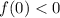 .
.
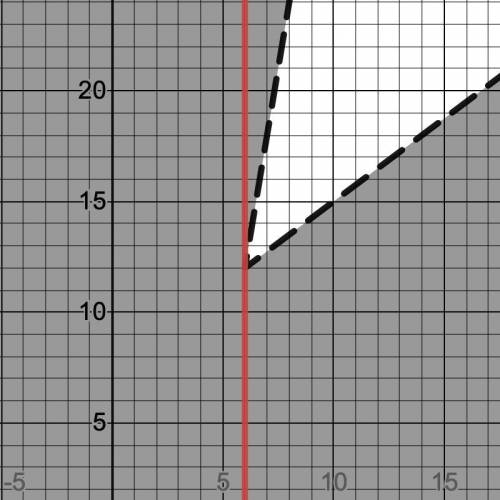
Тогда перейдем к неравенству:
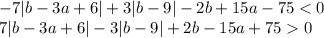
Построим его в координатах 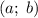 .
.
(см. прикрепленный файл)
Получили, что при 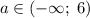 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 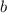 .
.
ответим теперь на вопрос задачи: ниже 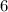 .
.
Задание выполнено!
764336, 853157, 854335, 348975, 356897, 853679, 279742, 741268, 7545677.